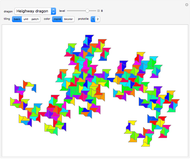
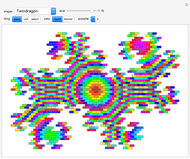
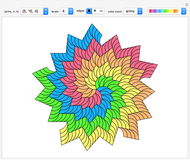
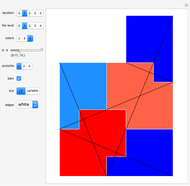
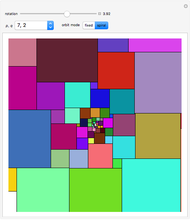
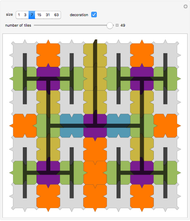
Tiling Dragons and Rep-tiles of Order Two

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
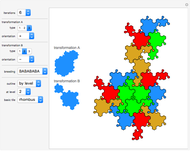
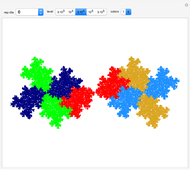
Dragons and rep-tiles of order two constructed by iterated function systems (IFS) of order two can tile the plane. But such a rep-tile can itself also be tiled by simple polygons. This results in a variety of tiling shapes from intermediate iteration steps. Well-known fractals like the Harter–Heighway dragon, Lévy dragon, twindragon and more can be tiled in this way.
Contributed by: Dieter Steemann (December 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
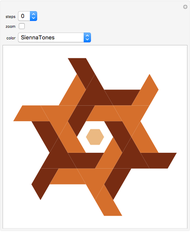
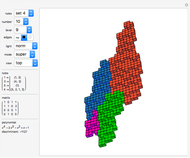
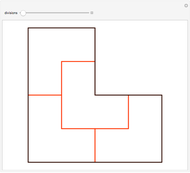
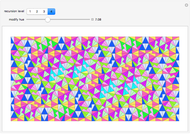
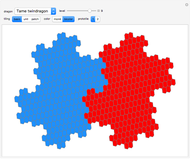
This Demonstration shows rep-tiles of order two, that is, plane figures that can be dissected into two congruent smaller figures, possibly by a reflection. Some of these are fractals. Such rep-tiles may tile the plane periodically; that is, they tile the plane without gaps or overlaps, using only multiple translations of one base figure. A tile that can be used for a periodic tiling is called a unit tile. Each rep-tile used here is defined by a two-part IFS. The final shape (an attractor) of an IFS is independent of the starting shape of the iteration. But it is possible to find initial prototiles so that every intermediate iteration level produces a new rep-tile that can tile the plane and is itself tiled by prototiles.
Only a few rep-tiles of order two fulfill these requirements. If the IFS is limited to rotation, translation and uniform scaling, six rep-tiles exist [1]: Lévy dragon [2], Harter–Heighway dragon [3], twindragon, tame twindragon, Cesaro triangle and rectangle.
As shown by Hinsley [4], further rep-tiles are possible when reflections are allowed. In his nomenclature, these are: scorpion, archno-dragon, tribolt and parallelogram. All except the tribolt are shown here. Still more rep-tiles are possible if nonuniform shearing and scaling transforms are allowed (I got such an IFS example from Roger Bagula). These rep-tiles resemble arrangements of twindragons and tame twindragons; four of them are included.
Controls
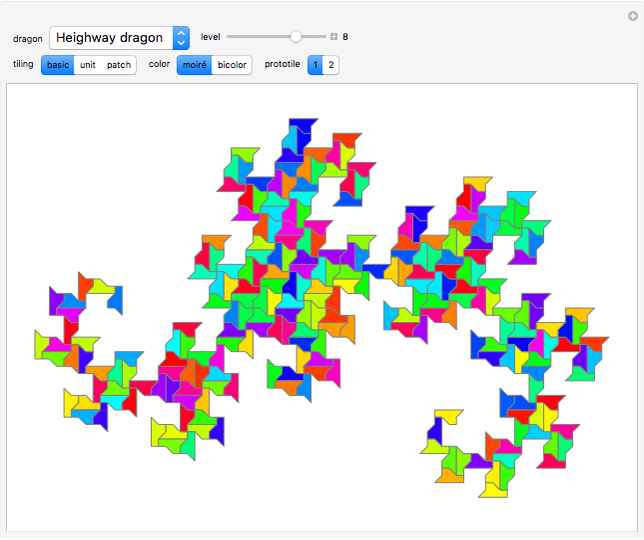
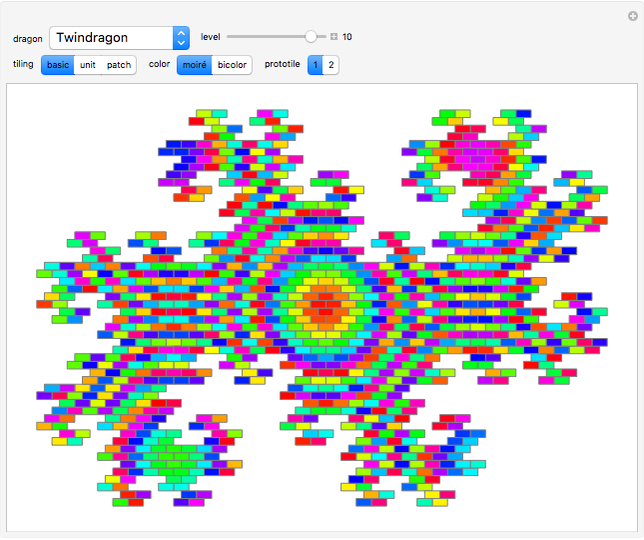
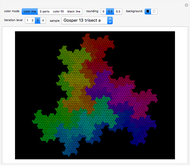
"tiling":
“basic”—Shows the rep-tile tiled by prototiles only. Iteration level 0 shows the prototile.
“unit”—When the basic tile is not a unit tile, two or more of them are combined into a unit tile.
“patch”—Combines two or more unit tiles periodically.
"prototile":
Two types of prototiles are provided for every rep-tile. Some of them result in partially unconnected basic tilings.
References
[1] S. M. Ngai, V. F. Sirvent, J. J. P. Veerman et al., "On 2-Reptiles in the Plane," Geometriae Dedicata, 82(1–3), 2000 pp. 325–344. doi:10.1023/A:1005206301454.
[2] L. Riddle. "Tiling the Plane with Lévy Dragon." (Dec 2, 2016). ecademy.agnesscott.edu/~lriddle/ifs/levy/tiling.htm.
[3] L. Riddle. "Heighway Dragon." (Dec 2, 2016) ecademy.agnesscott.edu/~lriddle/ifs/heighway/heighway.htm.
[4] S. R. Hinsley. "Dimers (2D)." (Dec 2, 2016) web.archive.org.
Permanent Citation