Torsional Pendulums

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
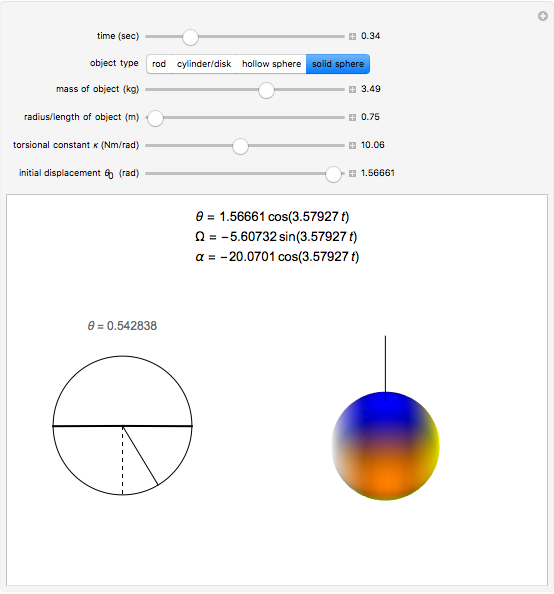
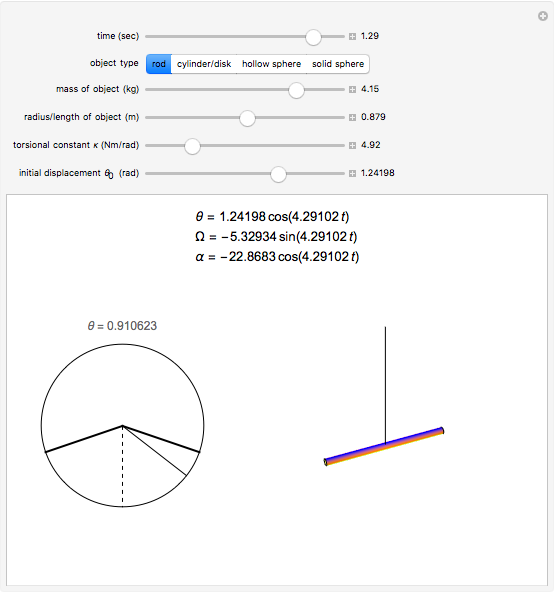
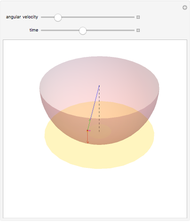
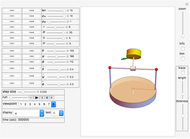
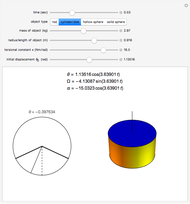
A torsional pendulum consists of an object suspended by a wire of a certain stiffness. The object is turned through an angle and released from rest, resulting in the harmonic motion of the object rotating back and forth. This Demonstration illustrates this type of harmonic motion, which follows Newton's second law for rotations,  . The torque of this pendulum is directly proportional to the angle it is turned by a factor of the torsional constant, which is a measure of the stiffness of the wire. Since
. The torque of this pendulum is directly proportional to the angle it is turned by a factor of the torsional constant, which is a measure of the stiffness of the wire. Since  ,
,  , which is a second-order differential equation. The solution of this equation as a function of time is
, which is a second-order differential equation. The solution of this equation as a function of time is  , where
, where  is the angular frequency.
is the angular frequency.
Contributed by: Ernest Lee (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
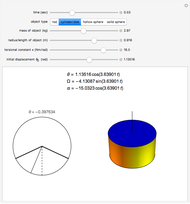
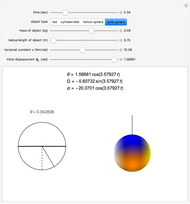
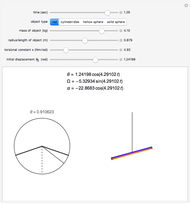
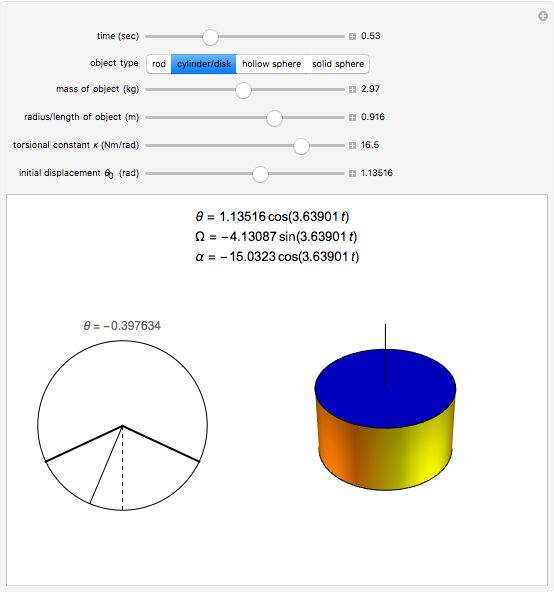
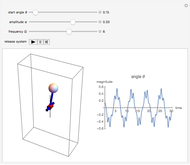
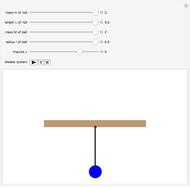
Select any of the four object types, and change the mass, radius/length, torsional constant, and initial angular displacement. The left graphic is a 2D representation of the angle through which the object is currently turned. The right graphic is a 3D depiction of the object rotating in space. Open the "time" slider and press play to animate the rotation of the object.
Permanent Citation