Tri: A Variant of Hex Played on a Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
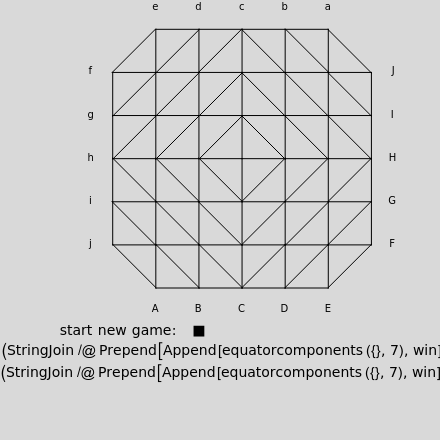
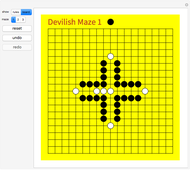
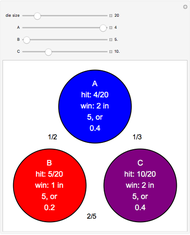
The game Tri is played on a sphere with a centrally symmetric triangulation where every vertex and every edge of the triangulation is initially uncolored. To move, a player (black or white) clicks an uncolored vertex to color it and its antipode. (Only pairs of antipodes on the equator show as two different points.) If the endpoints of an edge have the same color, the edge inherits that color. A player wins when a path of their color connects an antipodal pair of vertices.
Contributed by: Eugene Curtin (August 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
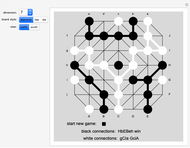
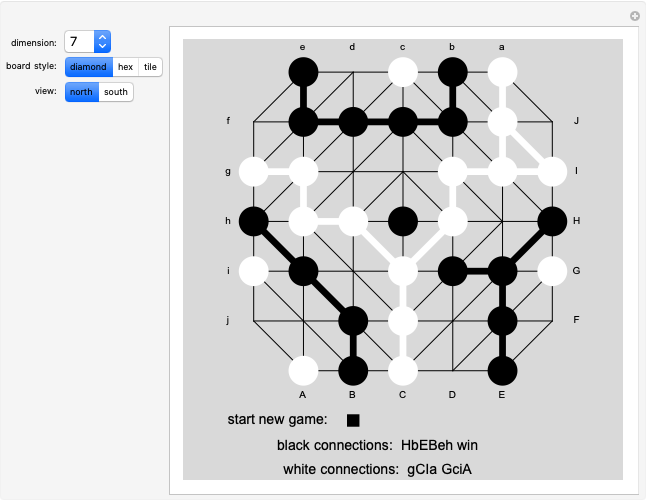
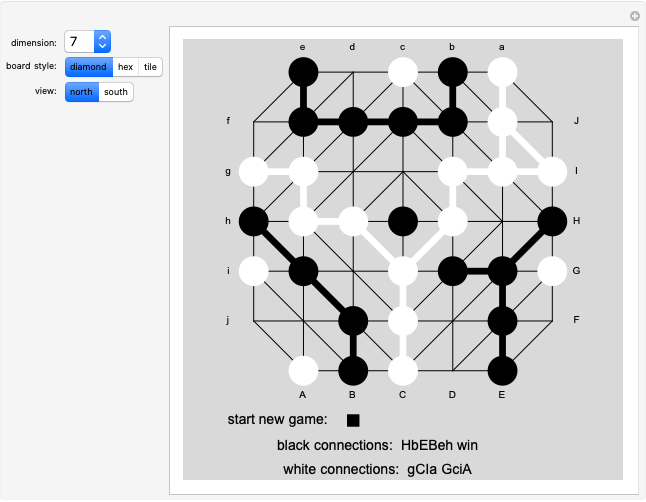
Snapshot 1: north view of a game in progress
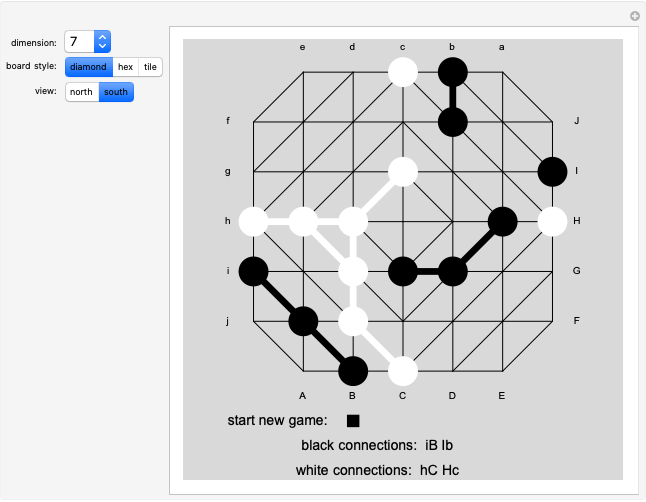
Snapshot 2: south view of the same game position
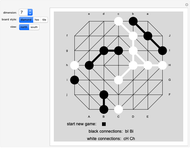
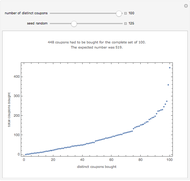
Snapshot 3: a position from a game with a hex triangulation board
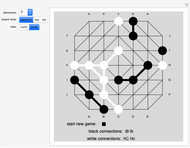
Snapshot 4: an equivalent position using a hex tiling board
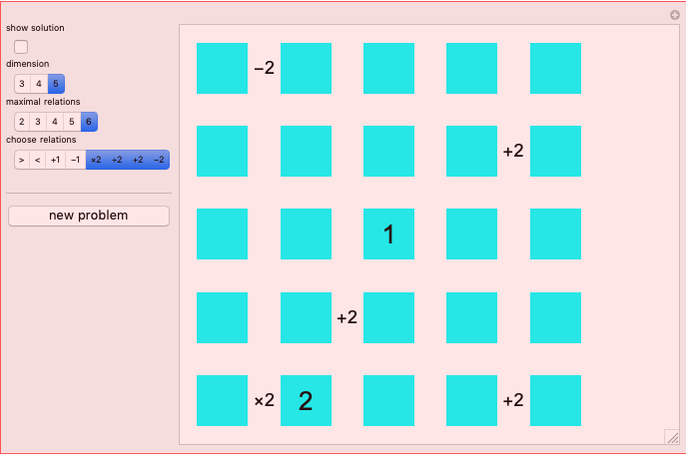
Snapshot 5: a division of the equatorial vertices resulting in a Hex game on a Tri board
To play the game of Tri, start with a centrally symmetric triangulation on the sphere. Two players, black and white, alternate in choosing an antipodal pair of vertices to color. If the endpoints of an edge are colored alike, the edge inherits that same color. A player wins the game when there is a path consisting of edges and vertices of their color connecting an antipodal pair of vertices.
This Demonstration allows the generation of boards with two different styles of triangulation that are here called "diamond" and "hex". The Demonstration shows only one hemisphere at a time, initially the north. The equatorial vertices are labeled. Antipodal pairs on the equator are labeled with the lower- and uppercase versions of the same letter. Which equatorial point each player has connected is recorded below the board. For example, if the northern hemisphere view shows black paths from h to B, E to H and b to e, the black connections are recorded as a single word with the letters B, E, H, b, e, h, in some order. The b-e path visible in the north implies a B-E path exists in the south, so the path h-B -E-H connects h and H. This black connection is thus recorded as a win.
The third board style option, "tile", results in a game entirely equivalent to the game on the hex triangulation of the same size. The vertices are replaced by hexagonal tiles, and the edges are omitted. Tiles are adjacent when they share a side. If the players began the game on a tile board by black playing on the first half of the labeled points in alphabetical order and white playing the second half, then the game reduces to a standard game of Hex. Because of this, Tri can be viewed as a generalization of Hex.
To play moves, click near an intersection point of the board in hex or diamond style, or near the center of a hexagon in tile style. If the point chosen is on the equator (the boundary of the board image) you will observe the point and its antipode both become colored. If the point is in the interior of the hemisphere view, you will initially observe only that point being colored. You may observe the coloring of its antipode by changing the view. The view can be toggled between north and south at any time, and moves may be made using either viewpoint. The controls allow the style to be changed at any point during a game. It makes no difference in the game if the style is changed from hex to tile or vice versa. If the change involves the diamond style, then the board edges change and the resulting game is not equivalent to the original. The "start new game" square can be clicked to clear the board for a new game.
When every vertex on a Tri board is colored either black or white, there must exist a path connecting an antipodal pair consisting of vertices that are all black or all white. Thus Tri cannot end in a draw, even dropping the requirement that players move alternately. Gale [1] showed the fact that Hex cannot end in a draw is equivalent to the Brouwer fixed-point theorem. Likewise, that Tri cannot end in a draw is equivalent to another famous theorem in topology, the Borsuk–Ulam theorem. It is a consequence of the Jordan curve theorem that it is not possible for both players to have connected an antipodal pair. As Hex can be played on a Tri board, the Tri theorems also imply the Hex theorems.
Reference
[1] D. Gale, "The Game of Hex and the Brouwer Fixed-Point Theorem," The American Mathematical Monthly, 86(10), 1979 pp. 818–827. doi:10.2307/2320146.
Permanent Citation