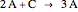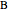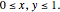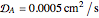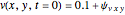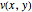Turing Pattern in a Reaction-Diffusion System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
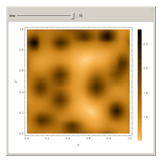
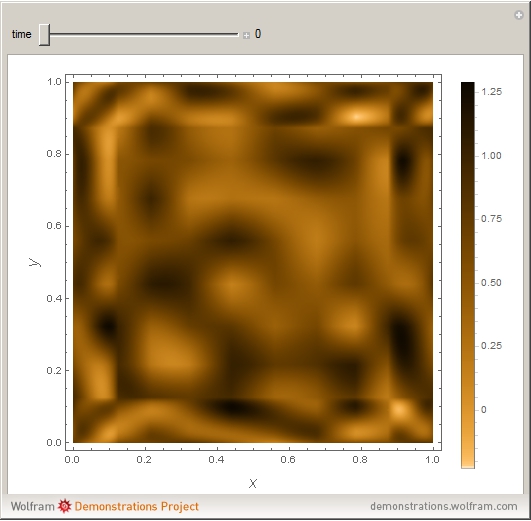
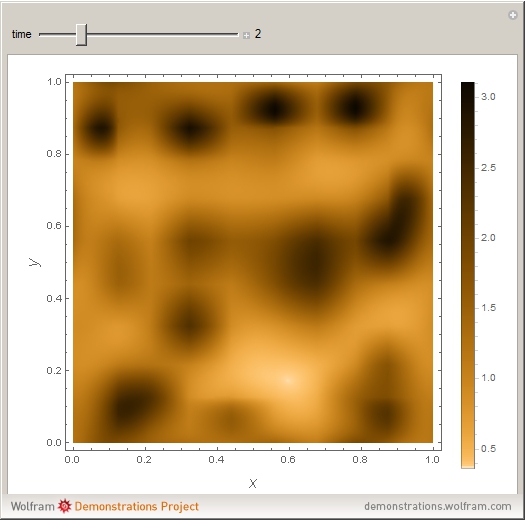
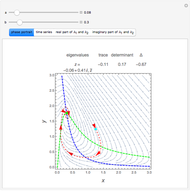
In the last few decades, developmental biologists have extensively used the reaction-diffusion model to explain pattern formation in living organisms. The original model was proposed by Alan Turing in 1952 [1]. The model is based on the idea that pattern formation results from two fundamental mechanisms: (1) coupled catalytic and autocatalytic reactions in a space element between two chemical species, an activator and an inhibitor, and (2) transfer of the interacting species to and from the neighboring space elements through a diffusional transport mechanism. Under appropriate reaction and diffusion conditions, a periodic pattern is formed from an initially homogeneous spatial distribution of activator and inhibitor [2, 3]. Examples of pattern formation can be found in biology, chemistry (the famous Belousov–Zhabotinskii reaction), physics, and mathematics [4, 5].
[more]
Contributed by: Housam Binous and Ahmed Bellagi (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] A. M. Turing, "The Chemical Basis of Morphogenesis," Philosophical Transactions of the Royal Society, 237(641), 1952 pp. 37–72.
[2] H. Meinhardt, The Algorithmic Beauty of Sea Shells, New York: Springer-Verlag, 1995.
[3] T. Miura and P. K. Maini, "Periodic Pattern Formation in Reaction-Diffusion Systems: An Introduction for Numerical Simulation," Anatomical Science International, 79(3), 2004 pp. 112–123.
[4] J. D. Murray, Mathematical Biology: I. An Introduction, 3rd ed., New York: Springer, 2002.
[5] J. D. Murray, Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed., New York: Springer, 2003.
Permanent Citation