Twisted Pyramid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
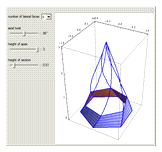
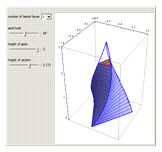
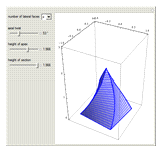
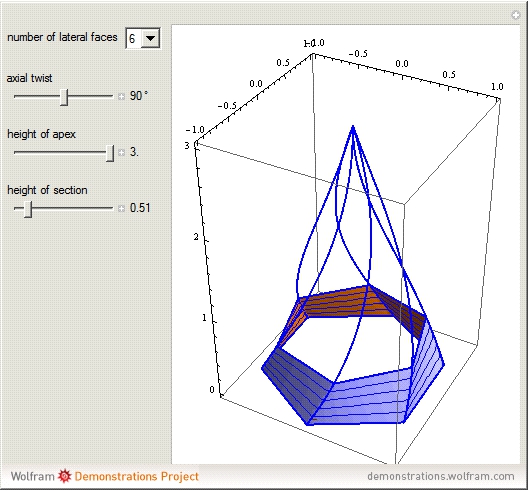
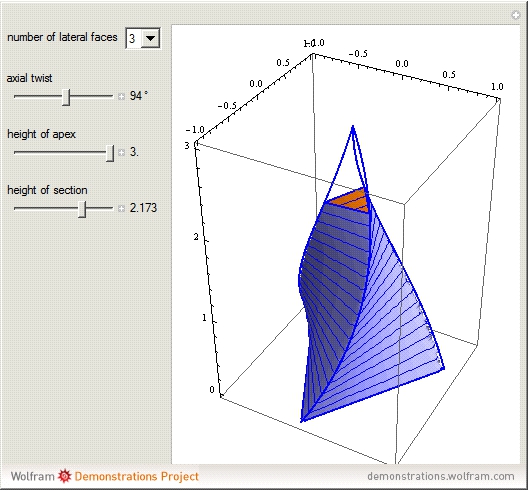
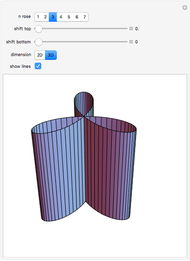
A regular pyramid is the result of connecting a regular polygon with an apex point directly above the center of the polygon. If you twist a regular pyramid, its lateral faces are no longer triangles but curved surfaces.
[more]
Contributed by: Erik Mahieu (March 2015)
Open content licensed under CC BY-NC-SA
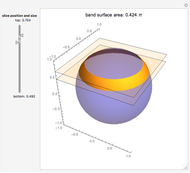
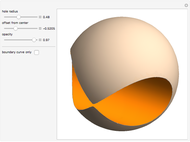
Snapshots
Details
A regular  -gon has polar equation
-gon has polar equation  , where
, where  is the radius of the circumcircle,
is the radius of the circumcircle,  is the number of sides,
is the number of sides,  is the angular offset, and
is the angular offset, and  is the polar angle.
is the polar angle.
Based on this, a regular  -gonal prism has the parametric equation
-gonal prism has the parametric equation  , with parameters
, with parameters  and
and  .
.
To get an  -gonal pyramid, replace the circumradius
-gonal pyramid, replace the circumradius  in
in  by
by  , where
, where  is the height of the pyramid.
is the height of the pyramid.
To twist the pyramid, replace the angular offset  by
by  , where
, where  is the total axial twist over the height of the pyramid.
is the total axial twist over the height of the pyramid.
Permanent Citation