Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

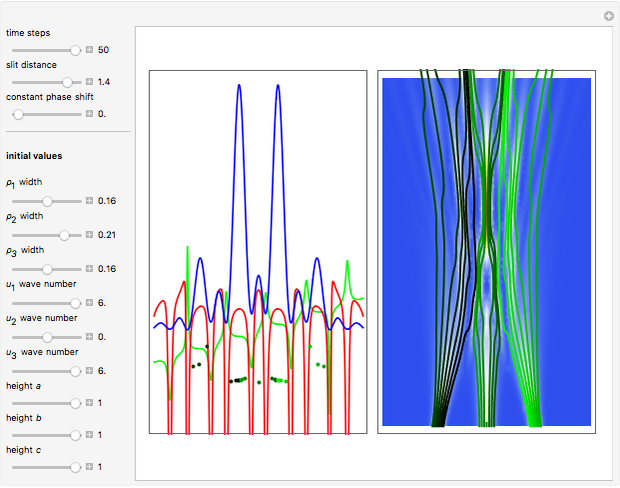
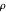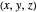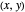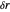Two Rotating Waves in de Broglie-Bohm Mechanics

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

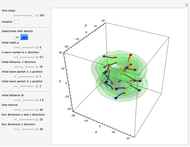
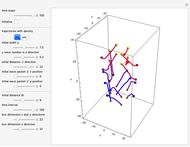
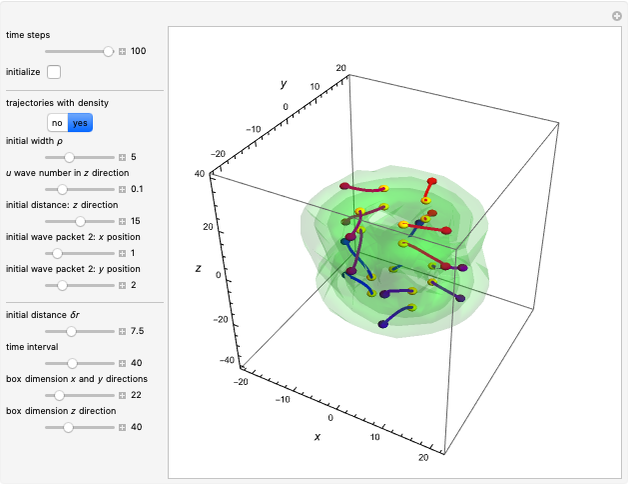
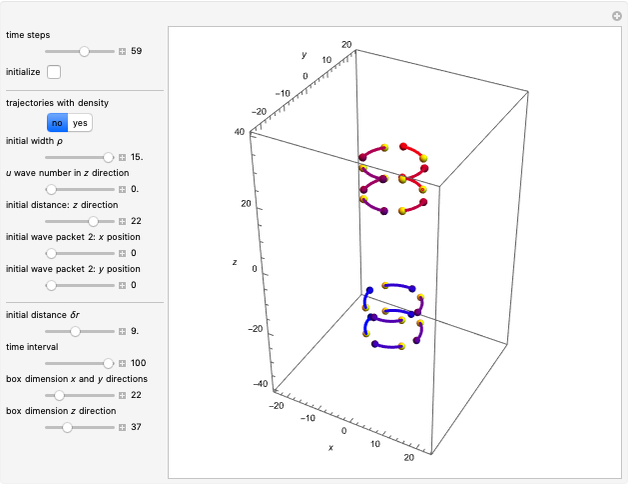
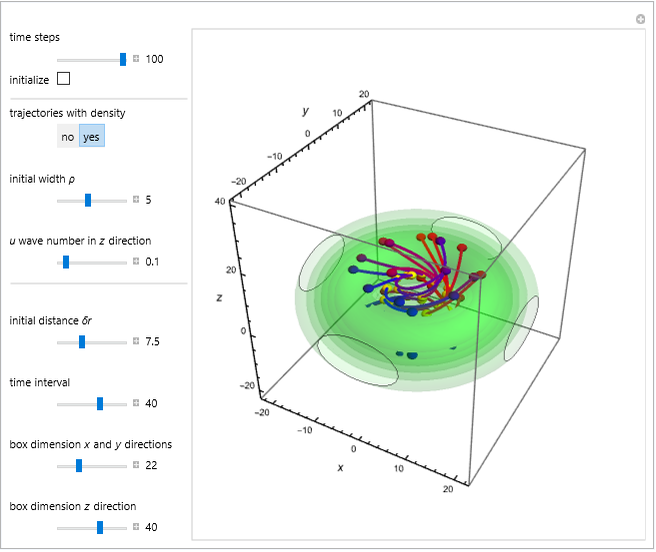
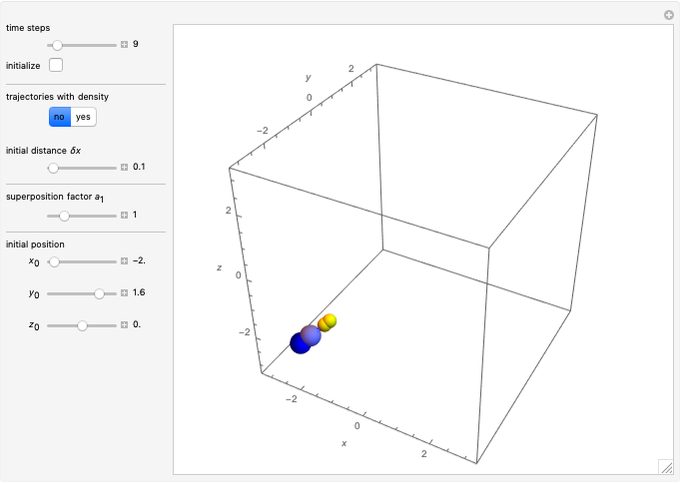
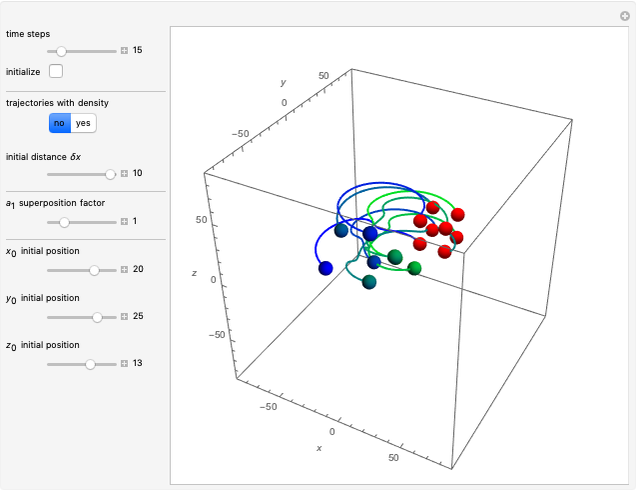
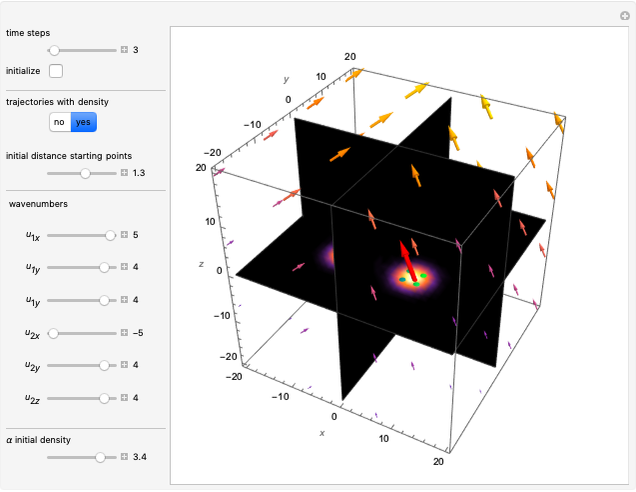
This Demonstration is an extended version of earlier work [1, 2] on two rotating wave packets with opposing angular velocities. This simple model can be used to visualize the time-dependent collision of two quantum particles, such as neutrons, in a collider experiment, by the de Broglie–Bohm approach. A collider is a particle accelerator based on two intersecting particle beams [3].

[more]

Consider two wave packets with specified "initial distance: direction" of the first particle and initial position of the second particle. These have the same component of momentum , with opposite sign.

In Bohmian mechanics [4, 5], the particles have well-defined trajectories in configuration space (CS), calculated from the total phase function. In practice, it is impossible to predict or control the quantum trajectories with complete precision. Real three-dimensional space is taken as the CS in this context.

In the de Broglie–Bohm approach, the possible orbits and velocities for this special wavefunction depend on the initial density , the wave number and initial position of the starting particles. The rotation around the axis is faster for a starting point closer to the origin.

The graphics show the wave density (if enabled), the initial starting points of 16 possible orbits (shown as small yellow spheres), the actual positions (shown as small colored spheres) and 16 possible trajectories with the initial distance .

You can vary the dimension of the box, the magnitude of the time interval, the initial distance and the initial position of the wave packet, the wave number , the initial width of the two particles and the initial distance between the starting trajectories determined by .

[less]

Contributed by: Klaus von Bloh (August 2022)
Open content licensed under CC BY-NC-SA

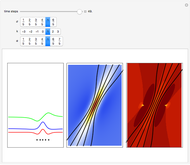
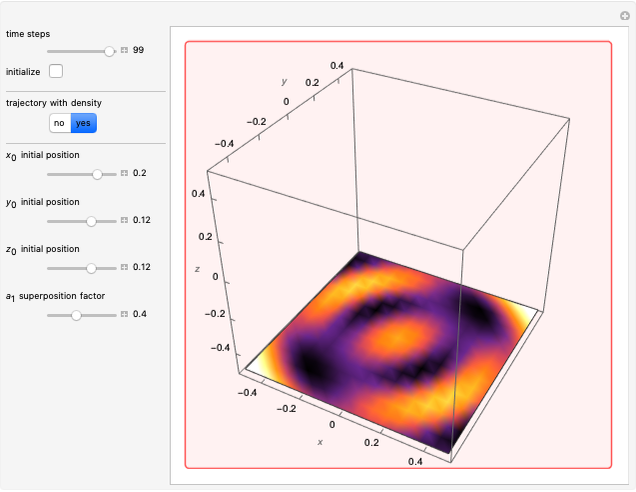
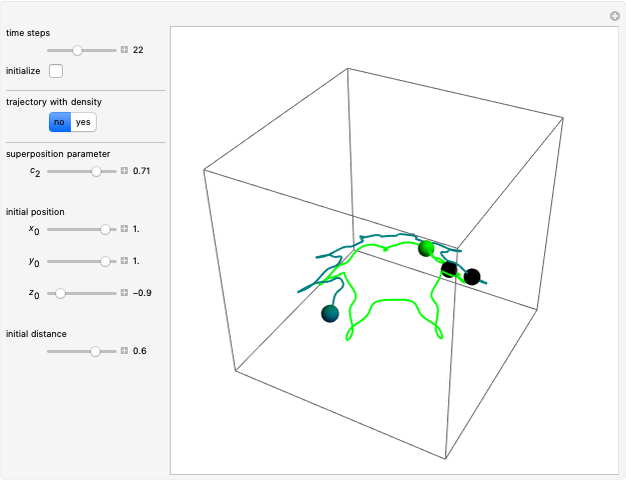
Snapshots

Details

Gaussian wave packets solutions obey the free-particle Schrödinger equation in cylindrical coordinates:

.

This can be converted to Cartesian coordinates (with atomic units: ):

.

This Demonstration uses two three-dimensional Gaussian wave packets, slightly different from [6]:

with , 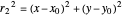with the initial 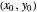position for the second wave packet, the initial width 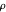, the initial position 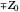for the two packets and the wave number 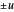in the direction.

Wave packets that rotate about their direction of motion could be constructed using derivatives with respect to :

.

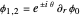If 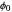is independent of , or in Cartesian coordinates generally:

,

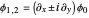which has an angular momentum component along the direction.

In this special case, the wave packets are given by:

.

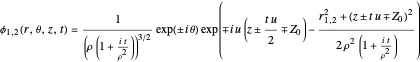In Cartesian coordinates, the components of the velocity can be determined from the gradient of the total phase function, which leads to the velocities (look at the code for further details).

When PlotPoints, AccuracyGoal, PrecisionGoal and MaxSteps are increased (if enabled), the results will be more accurate. The long-time behavior of the Bohm trajectories is exhibited in two YouTube videos [2, 7].

References

[1] K. von Bloh. "The Rotating Wave in de Broglie-Bohm Mechanics" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheRotatingWaveInDeBroglieBohmMechanics.

[2] K. von Bloh, The Rotating Wave in the de Broglie Bohm Approach (Bohmian Mechanics) [Video]. (Oct 25, 2021) www.youtube.com/watch?v=u_Cux59xiWA.

[3] Wikipedia. "Collider." (Dec 12, 2021) en.wikipedia.org/wiki/Collider.

[4] Bohmian-Mechanics.net. (Dec 13, 2021) bohmian-mechanics.net.

[5] S. Goldstein, "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy (Summer 2017 Edition). (Oct 25, 2021)plato.stanford.edu/entries/qm-bohm.

[6] J. Lekner, "Rotating Wavepackets," European Journal of Physics, 29(5), 2008 pp. 1121–1125. doi:10.1088/0143-0807/29/5/025.

[7] K. von Bloh, Two Rotating Waves in de Broglie–Bohm Mechanics [Video]. (Oct 25, 2021) www.youtube.com/watch?v=0ENHVy8eNqo.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send