Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Two Triangles of Equal Area on Either Side of an Angle Bisector

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

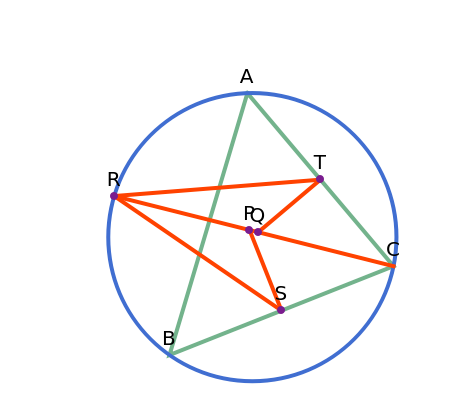
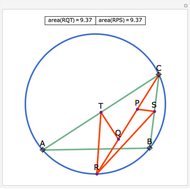
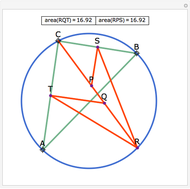
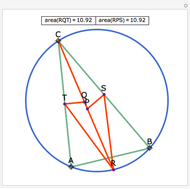
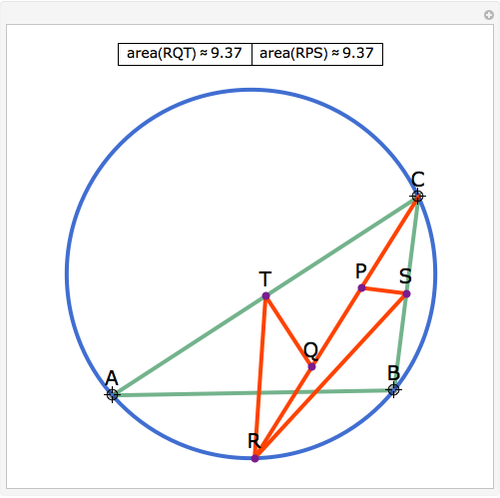
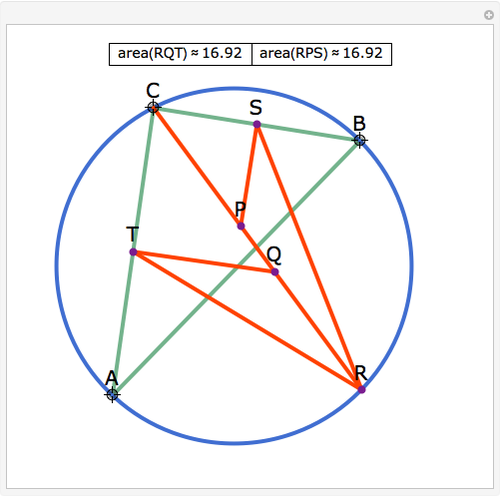
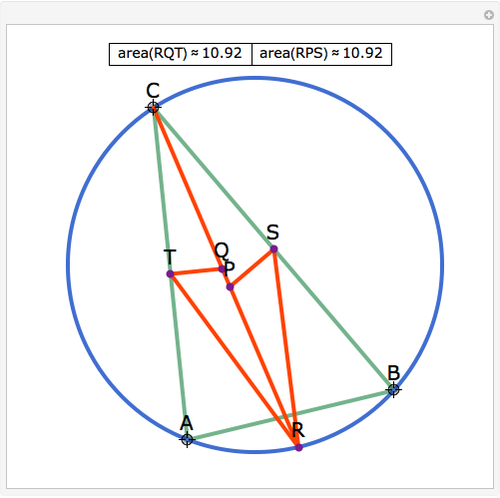
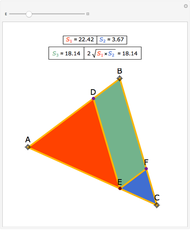
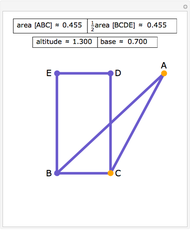
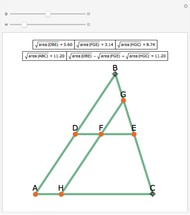
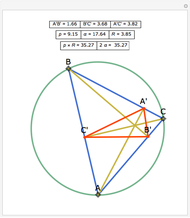
Let ABC be a triangle and let the angle bisector at vertex C intersect the circumcircle at R and the perpendicular bisectors of BC and AC at P and Q, respectively. Let the midpoints of BC and AC be S and T, respectively. Then RQT and RPS have equal area.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

See IMO 2007 shortlist geometry problem G1.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send