Wolfram Research

Mathematica MathWorld Wolfram Science More »

HOME

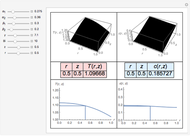
Unsteady-State Flow in a Tube by Orthogonal Collocation Method


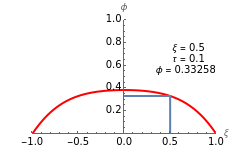
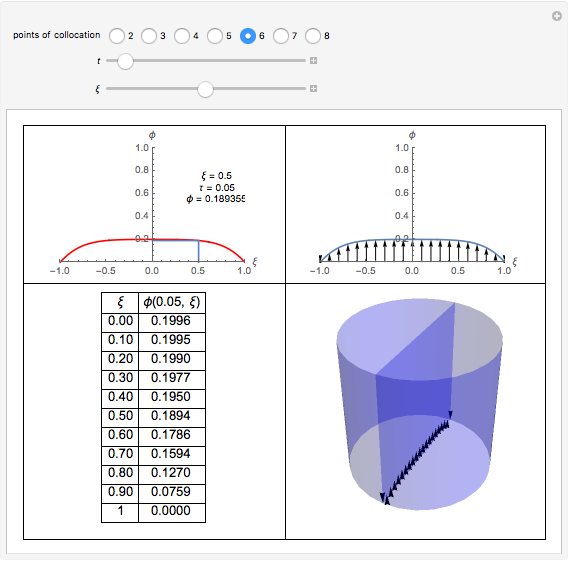
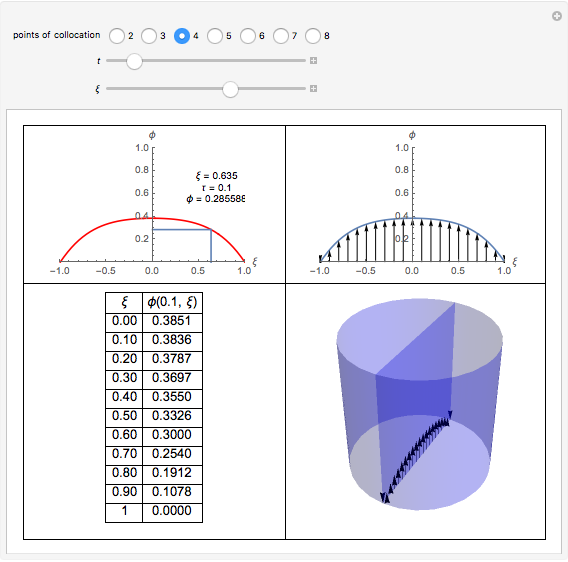
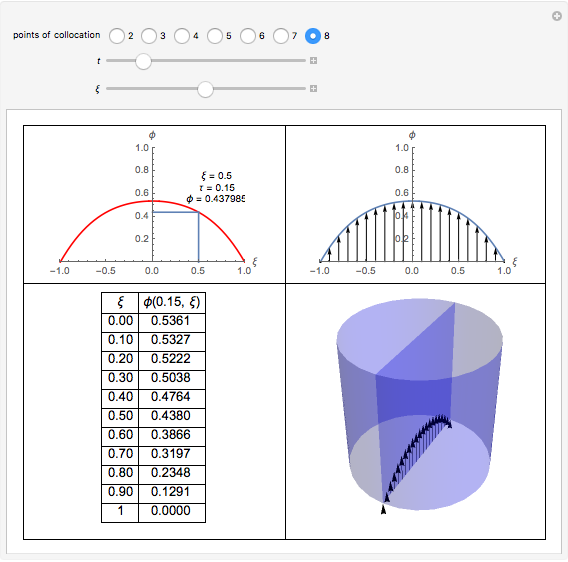
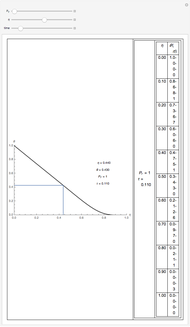
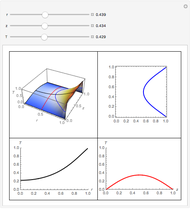
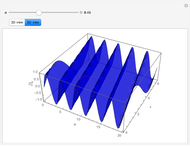
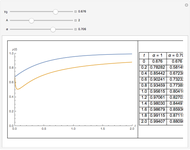
	In transport phenomena it is very common to encounter unsteady-state problems. This Demonstration describes the solution of a partial differential equation that describes unsteady-state flow in a tube, using an orthogonal collocation method.


	Contributed by: Jorge Gamaliel Frade Chávez

Unsteady flow in a tube is described by the following dimensionless partial differential equation:

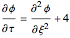with these boundary conditions:

and the initial condition:

In the partial differential equation

is nondimensional velocity,

is nondimensional time, and

is nondimensional position.

References: J. V. Villadsen and W. E. Stewart, "Solution of Boundary-Value Problems by Orthogonal Collocation," Chemical Enginering Science, 22, 1967 pp. 3981–3996.

R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley and Sons.

"Unsteady-State Flow in a Tube by Orthogonal Collocation Method" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/UnsteadyStateFlowInATubeByOrthogonalCollocationMethod/

Contributed by: Jorge Gamaliel Frade Chávez

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Browse all topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom