Viscosity in Glass Transitions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
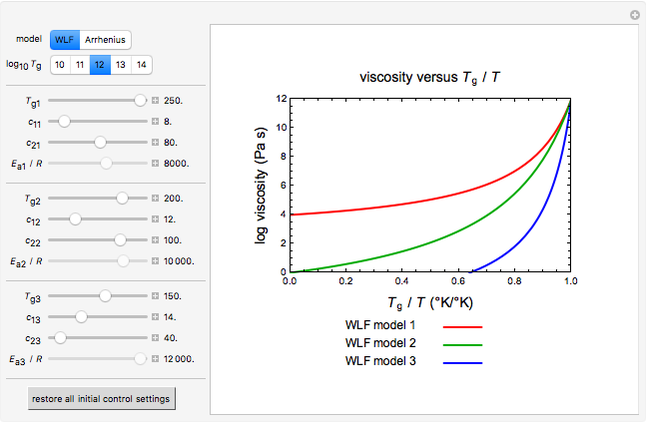
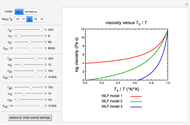
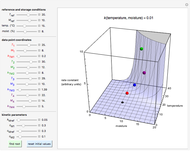
Glass transition is associated with a dramatic change in a material's viscosity. In the literature, there are plots of the viscosity versus 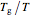 ratios (
ratios ( ) of several materials, all converging to a single point where
) of several materials, all converging to a single point where  and the viscosity is
and the viscosity is 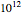 Pa s. Such plots can show the viscosity-temperature relationships of fragile and strong materials together for comparison. Since the glass transition temperature
Pa s. Such plots can show the viscosity-temperature relationships of fragile and strong materials together for comparison. Since the glass transition temperature 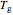 in such plots has been defined as the temperature at which the viscosity reaches
in such plots has been defined as the temperature at which the viscosity reaches that level, the convergence to a single point does not reveal any new information on the glass transition phenomenon itself. This is shown by plotting viscosity versus
that level, the convergence to a single point does not reveal any new information on the glass transition phenomenon itself. This is shown by plotting viscosity versus 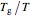 relationships governed by the WLF equation with different coefficients and
relationships governed by the WLF equation with different coefficients and 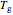 values with the assigned viscosity at
values with the assigned viscosity at  varying from
varying from 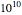 to
to 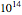 Pa s. The Arrhenius equation is also included, but only to show that the choice of the viscosity-temperature model does not affect the convergence.
Pa s. The Arrhenius equation is also included, but only to show that the choice of the viscosity-temperature model does not affect the convergence.
Contributed by: Mark D. Normand and Micha Peleg (June 2019)
Open content licensed under CC BY-NC-SA
Details
Snapshot 1: viscosity versus 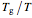 plots where
plots where 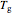 corresponds to viscosity of
corresponds to viscosity of 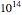 Pa s, generated with the WLF model having the same parameters used to generate the thumbnail
Pa s, generated with the WLF model having the same parameters used to generate the thumbnail
Snapshot 2: viscosity versus 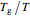 plots where
plots where 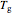 corresponds to viscosity of
corresponds to viscosity of 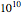 Pa s, generated with the WLF model with different parameters than those used to generate the thumbnail and Snapshot 1
Pa s, generated with the WLF model with different parameters than those used to generate the thumbnail and Snapshot 1
Snapshot 3: viscosity versus 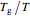 plots where
plots where 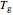 is defined by the viscosity of
is defined by the viscosity of 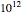 Pa s, generated with the Arrhenius model
Pa s, generated with the Arrhenius model
Snapshot 4: viscosity versus  plots where
plots where  corresponds to viscosity of
corresponds to viscosity of 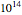 Pa s, generated with the Arrhenius model with different parameters than those used to generate Snapshot 3
Pa s, generated with the Arrhenius model with different parameters than those used to generate Snapshot 3
The object of this Demonstration is to show that the convergence of such curves occurs regardless of the chosen viscosity-temperature model, the magnitudes of its parameters, the 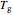 assigned to the materials and the chosen viscosity level that defines it.
assigned to the materials and the chosen viscosity level that defines it.
Perhaps the best-known viscosity-temperature model is the two-parameter WLF model [4], which for our purpose can be written in the form
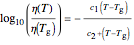 ,
,
where 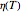 and
and 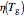 are the viscosities at temperatures
are the viscosities at temperatures  and
and 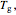 respectively, both in
respectively, both in 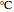 , and
, and  ,
, 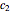 are constants. This model has been widely used to replace the single-parameter Arrhenius equation, which may only apply at higher temperatures. For our purpose, the Arrhenius equation can be written in the form
are constants. This model has been widely used to replace the single-parameter Arrhenius equation, which may only apply at higher temperatures. For our purpose, the Arrhenius equation can be written in the form

where the temperatures are in 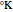 ,
, 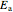 is the "energy of activation" and
is the "energy of activation" and 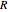 is the universal gas constant in commensurate units. It can be shown that if the absolute temperatures in the Arrhenius equation,
is the universal gas constant in commensurate units. It can be shown that if the absolute temperatures in the Arrhenius equation, 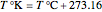 and
and 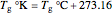 , are replaced by
, are replaced by 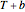 and
and 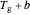 where
where  is an adjustable constant (all in
is an adjustable constant (all in 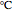 ), then the resulting expanded model becomes the same as the WLF model and thus also the VTF (or VFT) model, which has long been known as its equivalent [5].
), then the resulting expanded model becomes the same as the WLF model and thus also the VTF (or VFT) model, which has long been known as its equivalent [5].
For what follows we will use the original version of the Arrhenius model. While it is usually not appropriate for temperatures in the neighborhood of the glass transition, it can still show that the viscosity-temperature curve's convergence to a single point is independent of the chosen model.
To run the Demonstration, select the viscosity-temperature model, WLF or Arrhenius, with its setter bar and then choose the viscosity level that defines 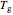 in the range from
in the range from 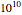 to
to  Pa s. Then choose the characteristics of three hypothetical or actual different materials, 1, 2 and 3, whose curves will be shown in red, green and blue, respectively. Use their sliders to enter or vary their
Pa s. Then choose the characteristics of three hypothetical or actual different materials, 1, 2 and 3, whose curves will be shown in red, green and blue, respectively. Use their sliders to enter or vary their 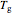 settings in
settings in 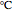 , the
, the 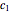 and
and 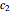 parameters of the WLF model, or the
parameters of the WLF model, or the 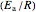 of the Arrhenius model.
of the Arrhenius model.
As expected, regardless of the particular settings, the three curves will always converge to the point where 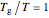 and the viscosity is that which is used to define the glass transition temperature.
and the viscosity is that which is used to define the glass transition temperature.
References
[1] Wikipedia. "Glass Transition." (Jun 6, 2019) en.wikipedia.org/wiki/Glass_transition.
[2] C. A. Angell, "Formation of Glasses from Liquids and Biopolymers," Science, 267(5206), 1995 pp. 1924–1935. www.jstor.org/stable/2886440.
[3] J. C. Mauro, Y. Yue, A. J. Ellison, P. K. Gupta and D. C. Allan, "Viscosity of Glass-Forming Liquids," Proceedings of the National Academy of Sciences, 106(47), 2009 pp. 19780–19784. doi:10.1073/pnas.0911705106.
[4] M. L. Williams, R. F. Landel and J. D. Ferry, "The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids," Journal of the American Chemical Society, 77(14), 1955 pp. 3701–3707. doi:10.1021/ja01619a008.
[5] M. Peleg, "Temperature-Viscosity Models Reassessed," Critical Reviews in Food Science and Nutrition, 58(15), 2018 pp. 2663–2672. doi:10.1080/10408398.2017.1325836.
Snapshots
Permanent Citation