Visualizing Atomic Orbitals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
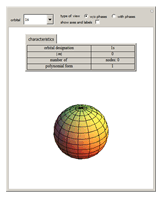
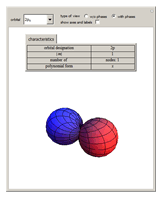
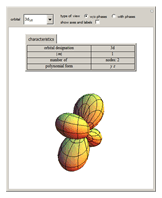
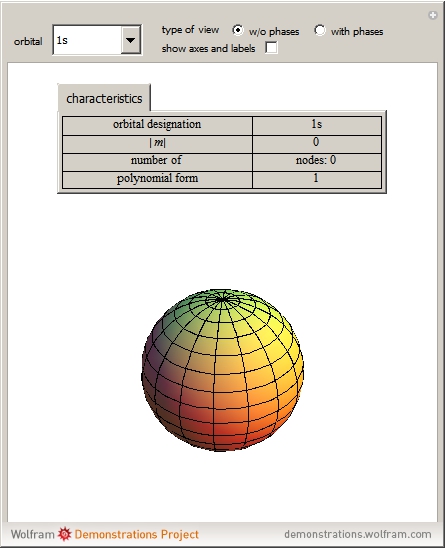
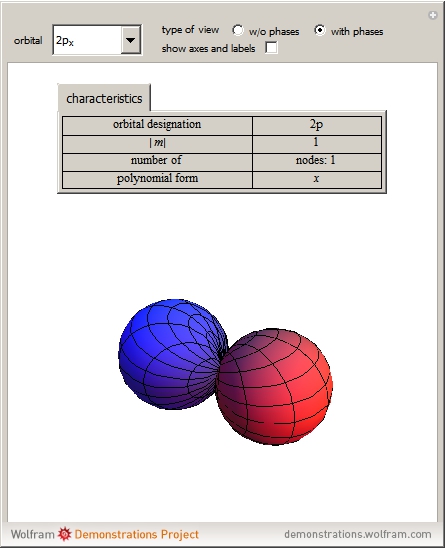
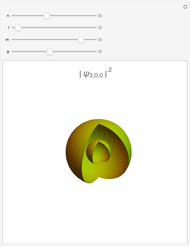
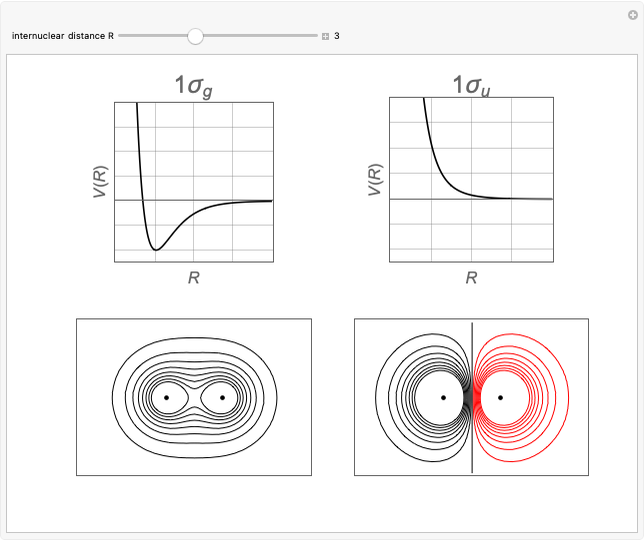
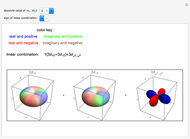
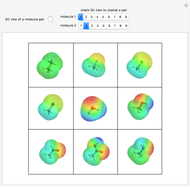
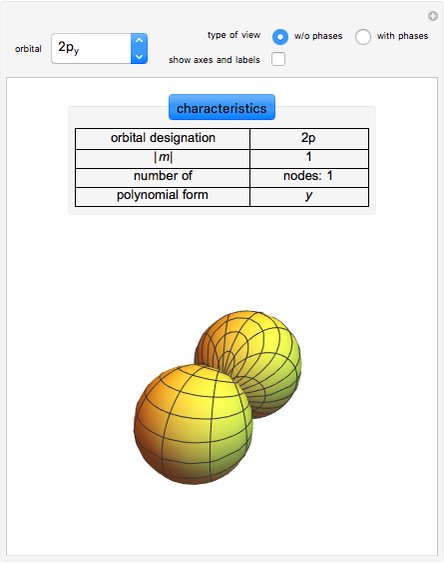
Atomic orbitals are the wavefunctions which are solutions of the Schrödinger equation for the hydrogen atom. The subset of atomic orbitals  ,
,  ,
,  and
and  are plotted in three dimensions to exhibit their characteristic shapes.
are plotted in three dimensions to exhibit their characteristic shapes.
Contributed by: Guenther Gsaller (June 2007)
(Institute of Organic Chemistry, Johannes Kepler University, Linz, Austria, http://www.jku.at/orc/)
Open content licensed under CC BY-NC-SA
Snapshots
Details
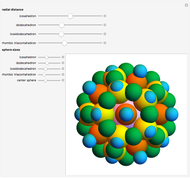
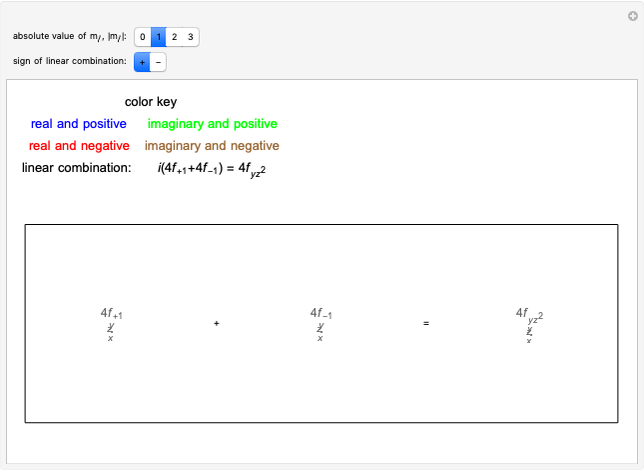
In chemistry orbitals can be classified according to their orientation in a rectangular coordinate system. The set of shapes in the snapshots is given for  and for combinations of
and for combinations of  .
.
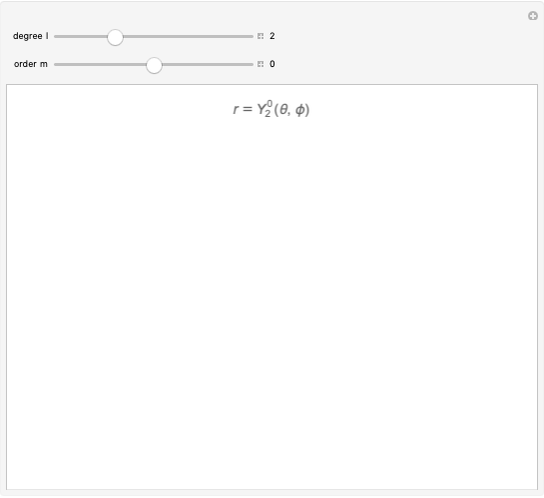
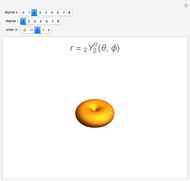
The three  -orbitals for a given value of
-orbitals for a given value of  are described by the values
are described by the values  ;
;  gives the
gives the  orbital. The angular functions for
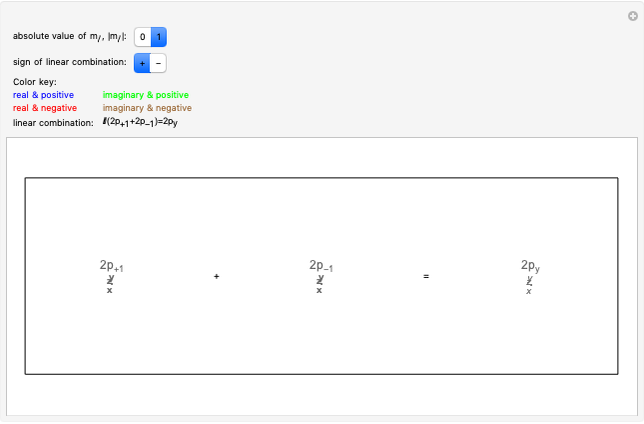
orbital. The angular functions for  are complex and depend on
are complex and depend on  ,
,  , or both. Pairwise linear combinations of complex spherical harmonics
, or both. Pairwise linear combinations of complex spherical harmonics  yield real functions, which can be plotted as boundary surfaces.
yield real functions, which can be plotted as boundary surfaces.
For  and
and  , for example, we have
, for example, we have
 and
and  .
.
The function pos inside OrbitalModel is shown at the link Problem with SphericalPlot3D plotting. It is used to attach signs to the positive or negative parts of the radial wavefunction. Then both parts are colored differently.
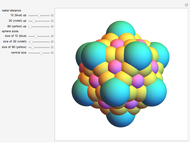
Alternative representations for the seven  orbitals can be written. In this Demonstration, the most commonly used convention was chosen [3].
orbitals can be written. In this Demonstration, the most commonly used convention was chosen [3].
References
[1] P. Atkins, R. Friedman, Molecular Quantum Mechanics, Oxford: Oxford University Press, 2011.
[2] R. King, "Atomic orbitals, symmetry, and coordination polyhedra," Coordination Chemistry Reviews, 197, 2000 pp. 141–168.
[3] M. Winter. "The Orbitron: a gallery of atomic orbitals and molecular orbitals on the WWW." (Jan 2013) http://winter.group.shef.ac.uk/orbitron/AOs/4f/index-gen.html.
Permanent Citation