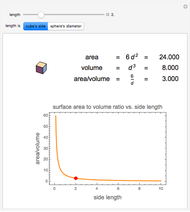
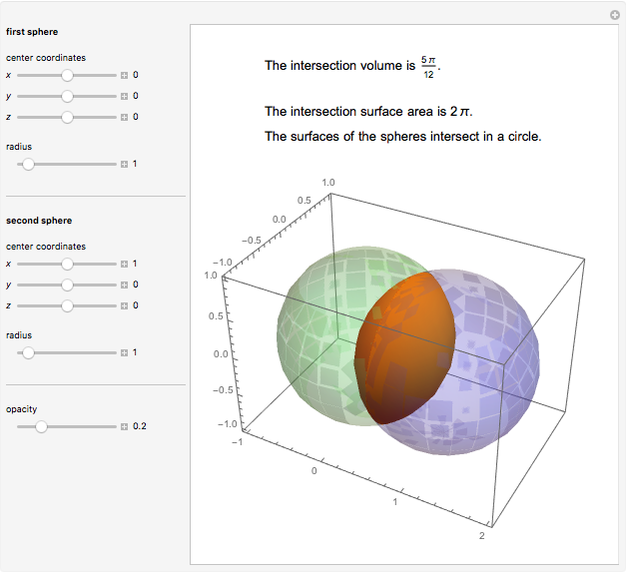
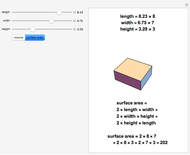
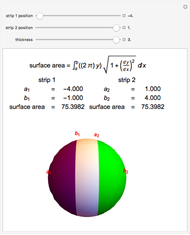
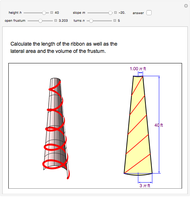
Volume under a Sphere Tangent to a Cone

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
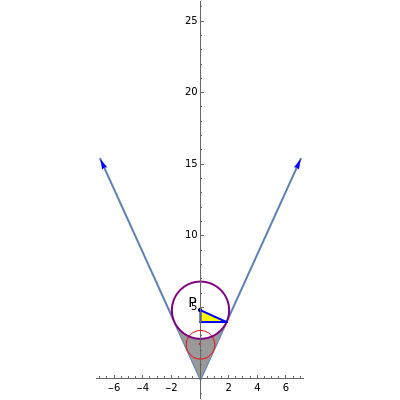
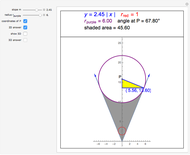
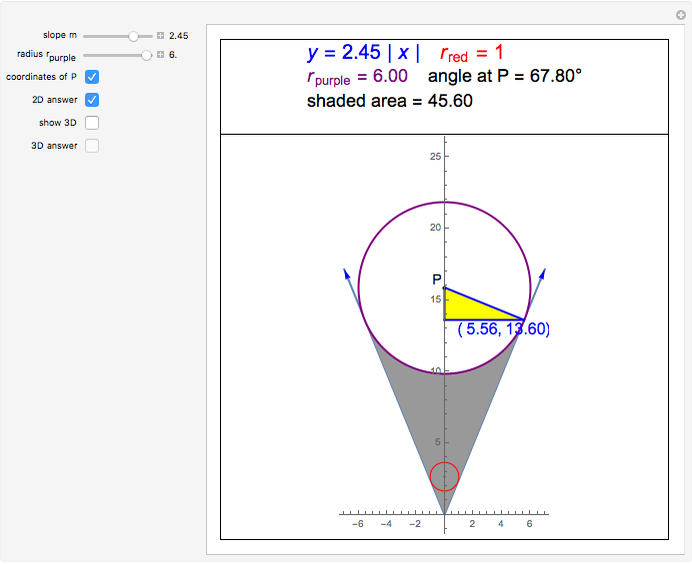
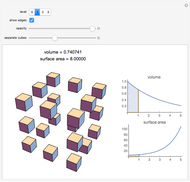
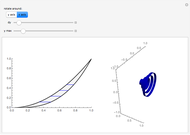
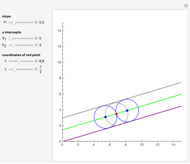
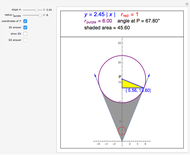
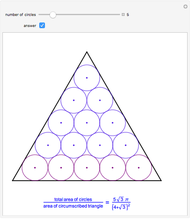
The red circle  with unit radius and center on the positive
with unit radius and center on the positive  axis is tangent to the lines through the origin with slopes
axis is tangent to the lines through the origin with slopes  .
.
Contributed by: Abraham Gadalla (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
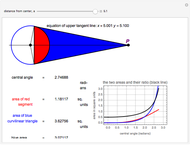
If the points of tangency are  and
and  , where
, where  is the slope, then the radius of the tangent circle at these points can be calculated to be
is the slope, then the radius of the tangent circle at these points can be calculated to be  , with corresponding tangent circle center at
, with corresponding tangent circle center at  .
.
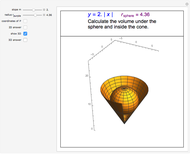
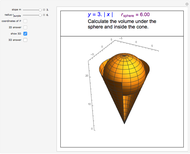
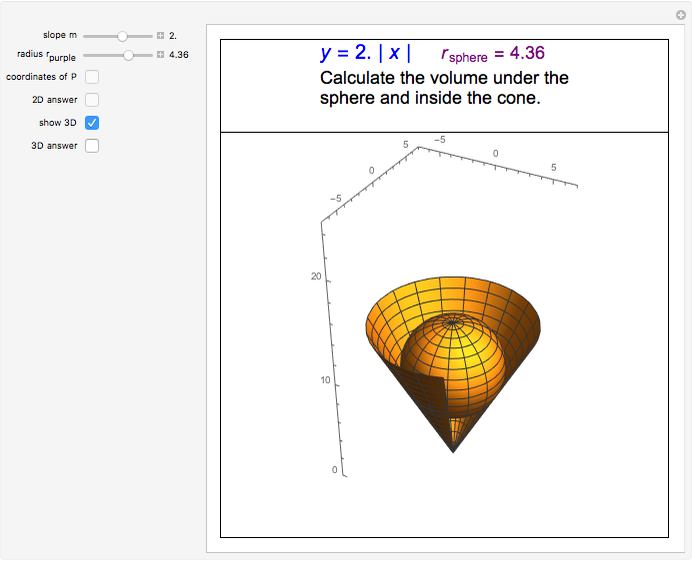
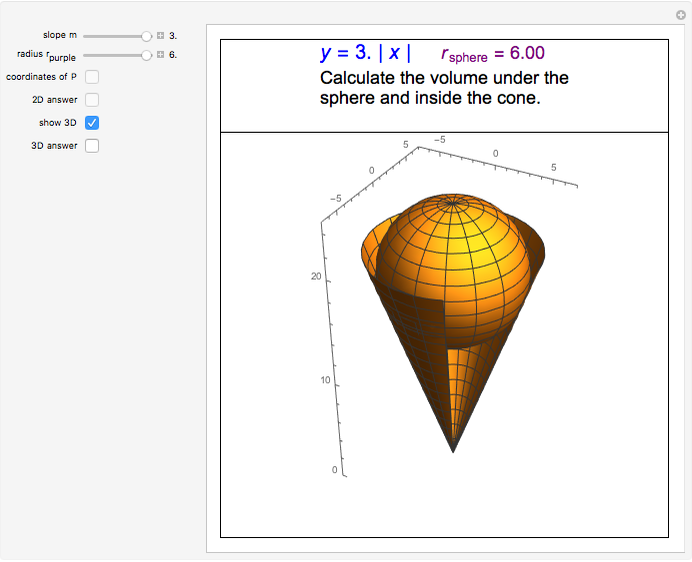
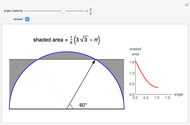
The volume under the sphere is equal to  , where:
, where:
1.  is the total volume resulting from rotating the region bounded by the line connecting the center of the circle
is the total volume resulting from rotating the region bounded by the line connecting the center of the circle  with the point of tangency
with the point of tangency  about the
about the  axis. This total volume is calculated using the shell method;
axis. This total volume is calculated using the shell method;  .
.
2.  is the volume of the spherical sector.
is the volume of the spherical sector.
The volume of a sector of a sphere with radius  is
is  , where
, where  is the height of the segment. In this case,
is the height of the segment. In this case,  . Therefore
. Therefore  ,
,
so  .
.
Finally, the required volume is  .
.
Permanent Citation