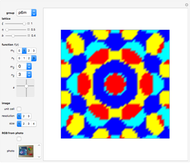
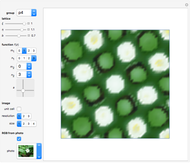
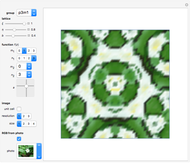
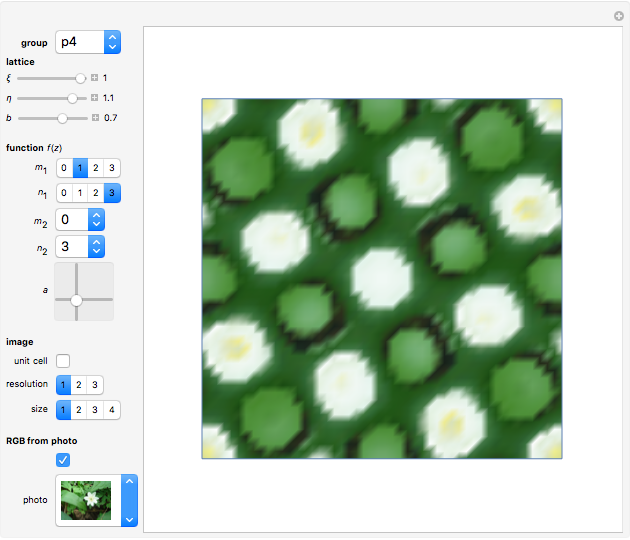
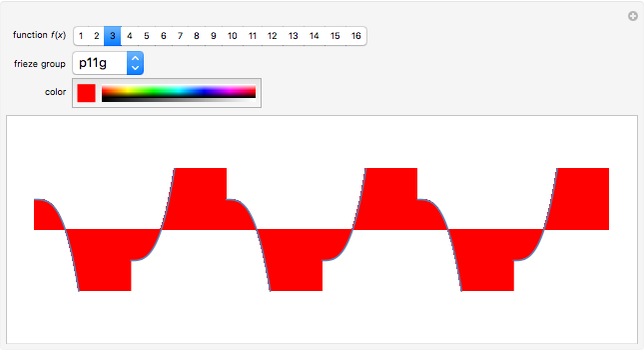
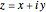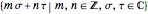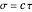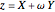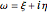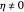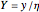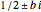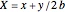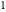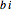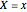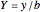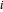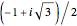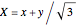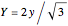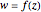Wallpaper Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
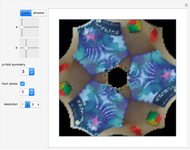
This Demonstration illustrates wallpaper groups using complex functions in the form of Fourier series  , where
, where  are called lattice waves, with only a small number of coefficients nonzero. A typical function of this type is
are called lattice waves, with only a small number of coefficients nonzero. A typical function of this type is 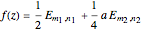 . In the event that the group contains a twofold rotation, we have
. In the event that the group contains a twofold rotation, we have 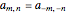 .
.
Contributed by: Izidor Hafner (March 2016)
Based on work by: Frank A. Farris
Open content licensed under CC BY-NC-SA
Snapshots
Details
Recipes for the wallpaper functions are given here [1, pp. 211–213];  is a reflection,
is a reflection,  a rotation, and
a rotation, and  a glide reflection.
a glide reflection.
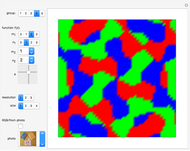
General lattice

Rhombic (centered) lattice
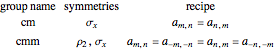
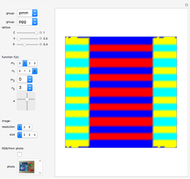
Rectangular lattice
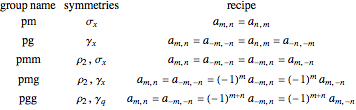
Here 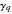 means vertical quarter-glide [1, p. 117].
means vertical quarter-glide [1, p. 117].
Square lattice
Wave packets to create fourfold symmetry are
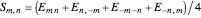 ,
, 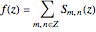 .
.

Using  for a central mirror,
for a central mirror, 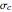 swaps
swaps 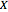 and
and 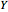 . The symmetry
. The symmetry 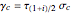 [1, pp. 99–101].
[1, pp. 99–101].
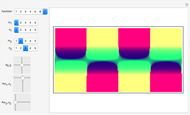
Hexagonal lattice
Wave packets to create threefold symmetry are
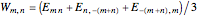 ,
, 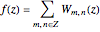 .
.
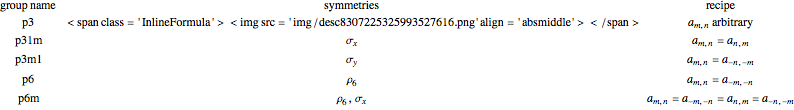
Reference
[1] Frank A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015.
Permanent Citation