Weber Points and Multifocal Ellipse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
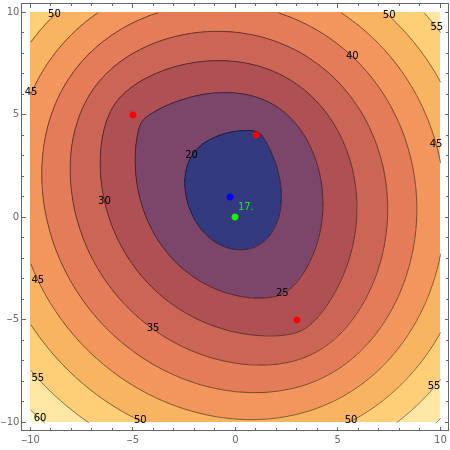
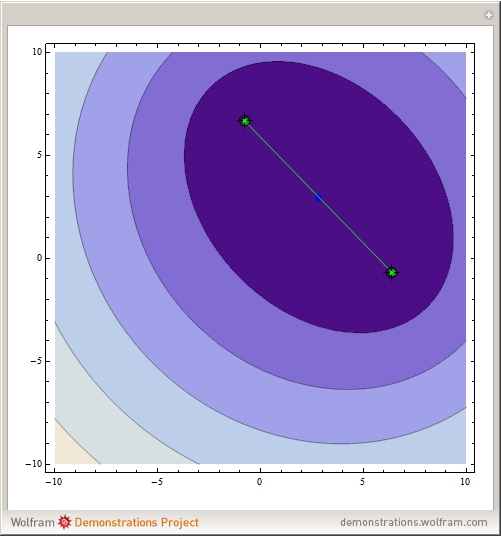
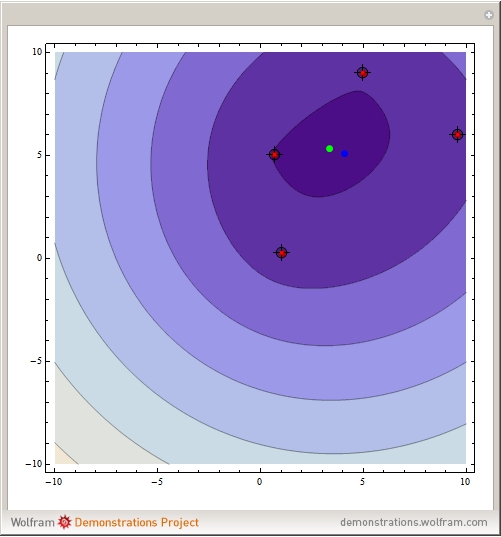
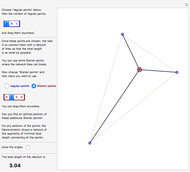
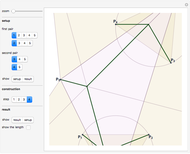
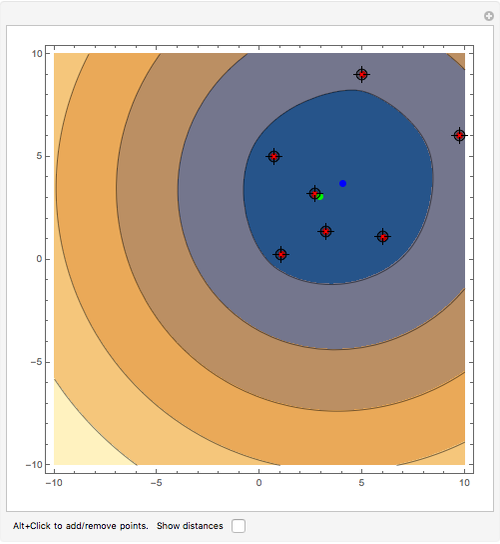
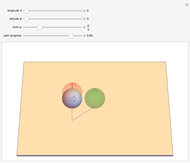
Where should a fire station be placed to minimize the total distance to  houses? This type of minimizing location is called the Weber point, and is shown in green for the red locations. Add or move the locators and notice the Weber point is often different than the mean location, shown in blue.
houses? This type of minimizing location is called the Weber point, and is shown in green for the red locations. Add or move the locators and notice the Weber point is often different than the mean location, shown in blue.
Contributed by: Aaron Becker (August 2014)
Open content licensed under CC BY-NC-SA
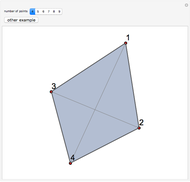
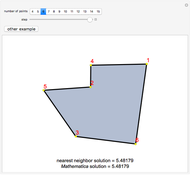
Snapshots
Details
The point  that minimizes distances from
that minimizes distances from  given points in a plane (the foci) is known as the Weber point; it is given by
given points in a plane (the foci) is known as the Weber point; it is given by
 , and the minimizing distance is
, and the minimizing distance is  .
.
If the points are not collinear, the Weber point is unique. If they are collinear, the Weber point is the set containing the line segment that is the convex hull of the points.
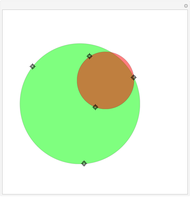
The locus of all points of the plane whose sum of distances to the  foci is a distance
foci is a distance  , where
, where  , is called a multifocal ellipse. The multifocal ellipse (also called an
, is called a multifocal ellipse. The multifocal ellipse (also called an  -ellipse) is a generalization of an ellipse with multiple foci. The multifocal ellipse for a total distance
-ellipse) is a generalization of an ellipse with multiple foci. The multifocal ellipse for a total distance  is defined as
is defined as
 .
.
The 1-ellipse is a circle and the 2-ellipse is a classic ellipse.
References
[1] E. J. Cockayne and Z. A. Melzak, "Euclidean Constructability in Graph-Minimization Problems," Mathematics Magazine, 42, 1969 pp. 206–208.
[2] C. Bajaj, "The Algebraic Degree of Geometric Optimization Problems," Discrete and Computational Geometry, 3(1), 1988 pp. 177–191.
[3] T. Kupitz and H. Martini, "Geometric Aspects of the Generalized Fermat–Torricelli Problem," Bolyai Society Mathematical Studies, 6, 1997 pp. 55–129.
Permanent Citation