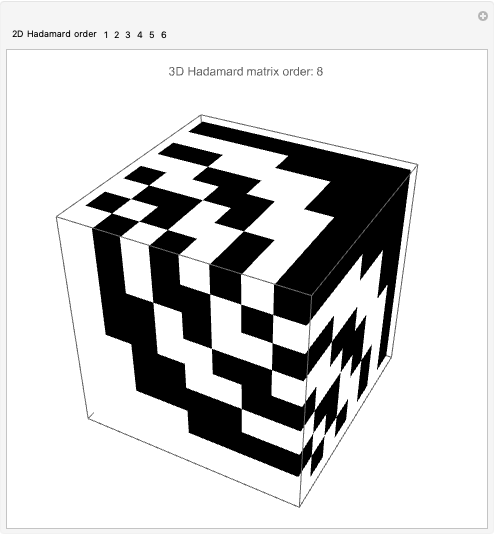
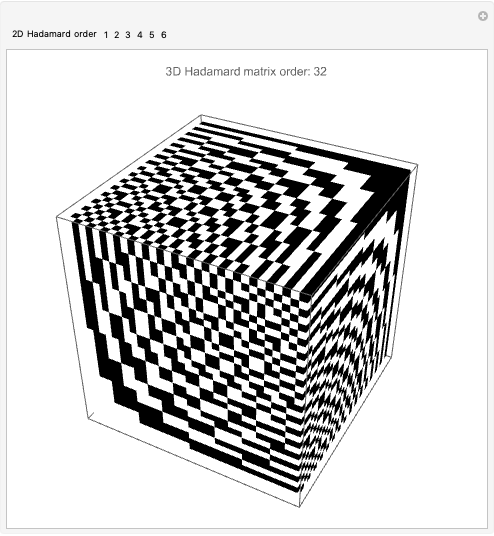
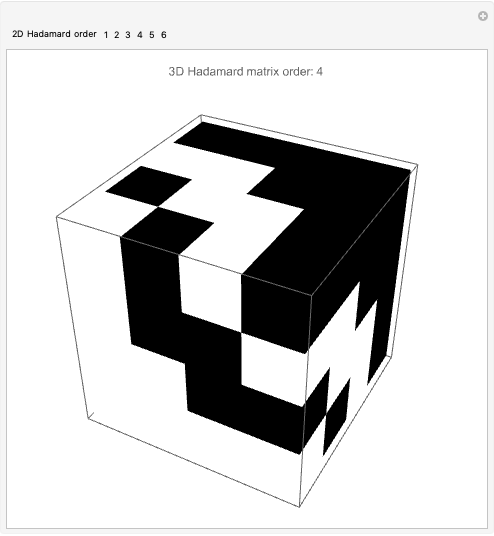
Yang's Construction of 3D Hadamard Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
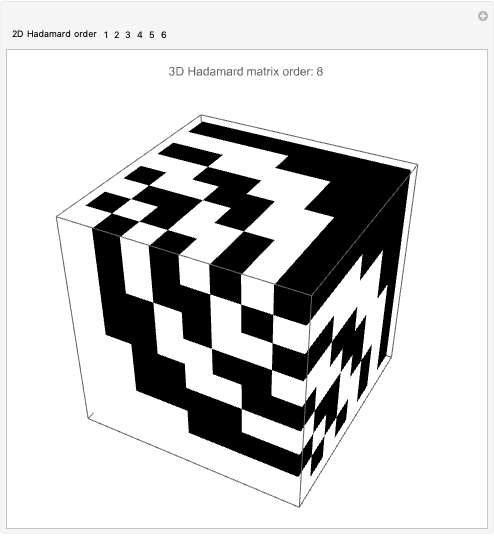
3D Hadamard matrices (cubes), are hypermatrices in which the rows, columns and slices are all mutually orthogonal. They have found application in optics [1, 2]. They add an additional dimension, thus one more degree of freedom, which can be exploited in modern orthogonal frequency-division multiplexing (OFDM/5G+RF) systems. Channel coding involves parameters such as frequency, time, phase and polarization. Hypermatrices are equivalent to tensors. See [3] for some of the original definitions of hyperdeterminants by Cayley. Multilinear algebras and high-order tensor algebras have not yet been exploited by the wireless signal processing community. I think this will change. In 1996, Yang developed a construction method for 3D Hadamard matrices based on 2D Hadamard matrices [4]. This Demonstration illustrates Yang's construction method. To extend this code to complex cubical Hadamard matrices, see [5].
Contributed by: Phil Neumiller (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] K. Latham, C. Samson, J. Woodacre, E. Simpson, R. Zemp and J. A. Brown, "A New 3D Imaging Technique Integrating Ultrafast Compounding, Hadamard Encoding, and Reconfigurable Fresnel Lensing, Demonstrated on a 128-Element, Crossed Electrode Endoscope," in 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, Piscataway, NJ: IEEE, 2019 pp. 2052–2055. doi:10.1109/ULTSYM.2019.8926257.
[2] N. S. Rao, S. H. Shruthi, D. Achutha, M. K. Dileep, R. Sandeep and D. L. Girijamba, "Perceptual Video Hashing Using 3D Hadamard Transformation," in 2017 International Conference on Current Trends in Computer, Electrical, Electronics and Communication (CTCEEC), Mysore, India, Piscataway, NJ: IEEE, 2017 pp. 477–480, doi:10.1109/CTCEEC.2017.8455022.
[3] Wikipedia. "Hyperdeterminant." (Nov 10, 2021) en.wikipedia.org/wiki/Hyperdeterminant.
[4] Y. Yang, Theory and Applications of Higher-Dimensional Hadamard Matrices, New York: Science Press, 2001.
[5] B. Lantz and M. Zowada, (2012) "An Overview of Complex Hadamard Cubes," Rose-Hulman Undergraduate Mathematics Journal, 13(2), 2012 Article 3. scholar.rose-hulman.edu/rhumj/vol13/iss2/3.
Permanent Citation