Biradial Matrix

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
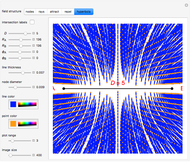
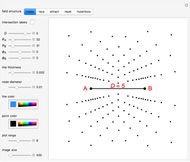
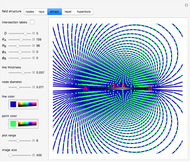
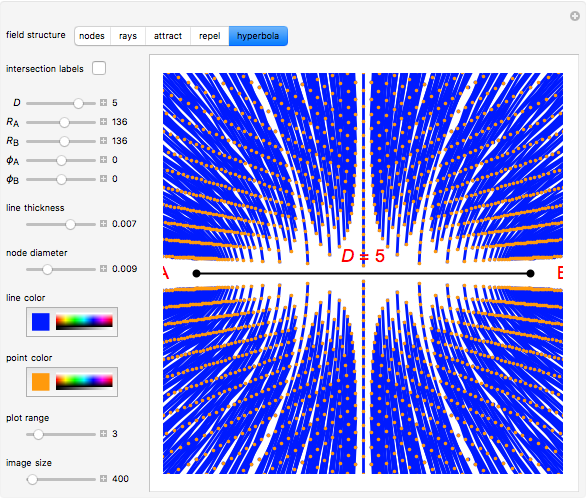
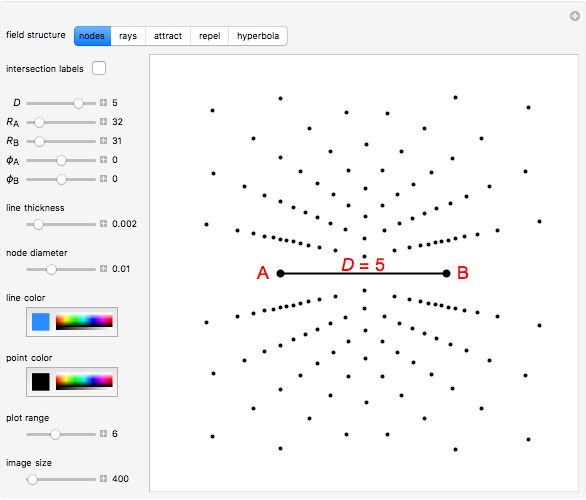
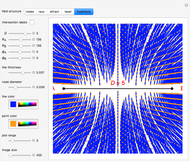
A biradial matrix consists of two sets of equally spaced radial lines separated by a distance 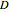 . Use the "nodes" or "rays" buttons to change the display. The rays (nodes) can be indexed from zero starting at the
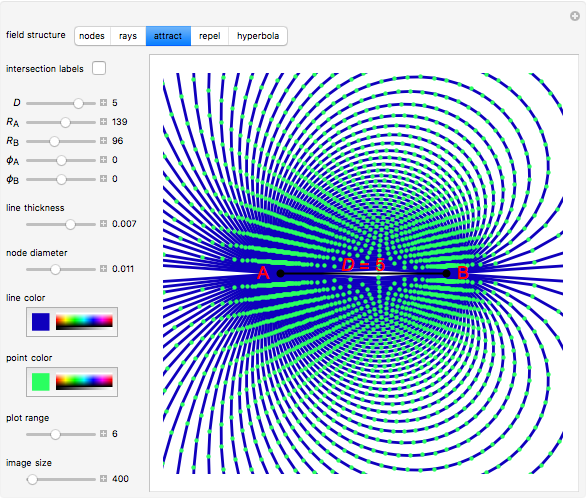
. Use the "nodes" or "rays" buttons to change the display. The rays (nodes) can be indexed from zero starting at the 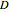 segment, creating a biradial coordinate system with coordinate pairings at the nodes; check "intersection labels" to see their values. By adhering to specific connection algorithms, fundamental field structures are set with the "attract", "repel" and "hyperbola" buttons. The number of rays from each pole can be set using the sliders
segment, creating a biradial coordinate system with coordinate pairings at the nodes; check "intersection labels" to see their values. By adhering to specific connection algorithms, fundamental field structures are set with the "attract", "repel" and "hyperbola" buttons. The number of rays from each pole can be set using the sliders  and
and 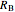 , which changes the subsequent field structures. The angular phase relation between the poles (defined elsewhere) can be set with the sliders
, which changes the subsequent field structures. The angular phase relation between the poles (defined elsewhere) can be set with the sliders 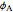 and
and 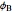 . This geometric construct has many applications in physics. The "line thickness" and "node diameter" sliders vary the thickness of the lines and diameter of the nodes.
. This geometric construct has many applications in physics. The "line thickness" and "node diameter" sliders vary the thickness of the lines and diameter of the nodes.
Contributed by: Russell Kramer (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The included angles from poles 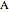 and
and 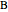 are designated as
are designated as  and
and  .
. 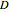 is the distance between poles
is the distance between poles 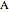 and
and 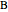 . There are numerous other variables that can be assigned to various segment lengths and other internal angles of the trapezoids defined by the intersecting rays. From this initial set of variables, an inverse-square equation based on the distance
. There are numerous other variables that can be assigned to various segment lengths and other internal angles of the trapezoids defined by the intersecting rays. From this initial set of variables, an inverse-square equation based on the distance 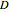 is derived, which corresponds to the field density as illustrated by the attraction, repulsion and hyperbola field lines. The nodes defined by the intersections of the rays can be designated with a biradial coordinate system allowing for a mathematical description of the field lines. These nodes and the resulting field lines appear related to the space networks described by Wolfram in [1]. The harmonic series is derived from the upper limit of rays from each pole in relation to the
is derived, which corresponds to the field density as illustrated by the attraction, repulsion and hyperbola field lines. The nodes defined by the intersections of the rays can be designated with a biradial coordinate system allowing for a mathematical description of the field lines. These nodes and the resulting field lines appear related to the space networks described by Wolfram in [1]. The harmonic series is derived from the upper limit of rays from each pole in relation to the 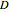 segment, indicating an underlying harmonic structure of the biradial matrix where the coordinate pairings also represent the ratios of the harmonic overtone series. The
segment, indicating an underlying harmonic structure of the biradial matrix where the coordinate pairings also represent the ratios of the harmonic overtone series. The 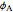 and
and 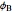 sliders alter the "phase relation", which is related to the rotation of either or both poles
sliders alter the "phase relation", which is related to the rotation of either or both poles 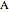 and
and 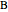 . As a conceptual model and harmonic coordinate system, the biradial matrix has many applications in physics. It is possible, for example, to define the gravitational equilibrium zone between two masses using the biradial matrix.
. As a conceptual model and harmonic coordinate system, the biradial matrix has many applications in physics. It is possible, for example, to define the gravitational equilibrium zone between two masses using the biradial matrix.
References
[1] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, Inc., 2002.
[2] R. Kramer. "Project #1: The Genesis Field and the Harmonic Structure of Space-Time." (Mar 9, 2017) www.bi-radialmatrixintro.com.
Permanent Citation