Boolean NK Networks

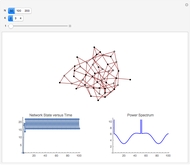
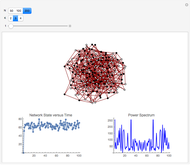
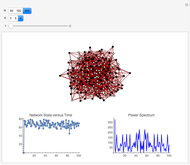
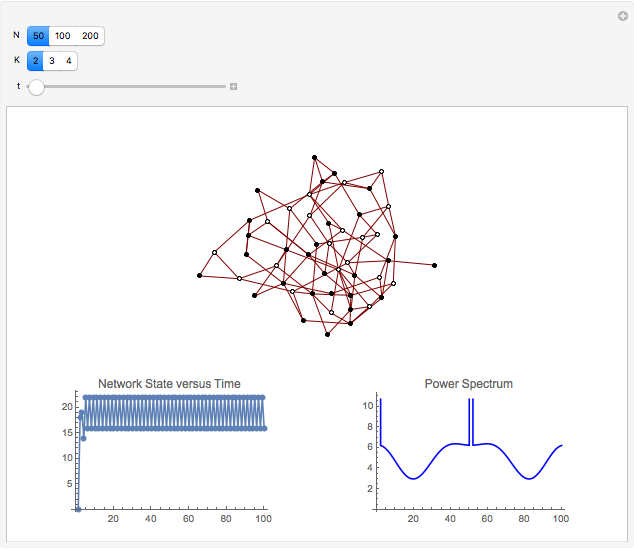
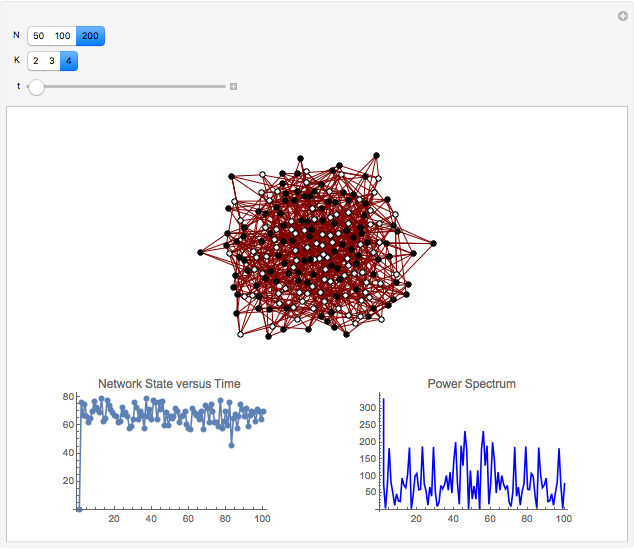
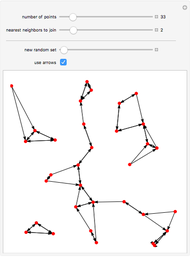
Boolean NK networks are networks whose nodes can be in one of two states (on or off) at any particular time in their dynamical evolution. The dynamics of Boolean NK networks are determined by two parameters (, which defines the number of nodes in the network, and , which defines the number of directional links between nodes) and a rule table for each node that specifies the state of the node at time step given the states of the connecting nodes at time step . In this Demonstration, each node is randomly assigned both an initial state and a rule table. Different values of and result in different network dynamics, which can be seen in the plot of network state (defined as the Hamming distance between the network's present state and initial state) versus time and the power spectrum of this plot. By varying , you can directly observe the real-time evolution of the network, which appears as a system of blinking lights.