Cycloidal Path of a Charged Particle in Uniform Perpendicular Electric and Magnetic Fields

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
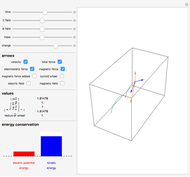
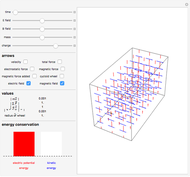
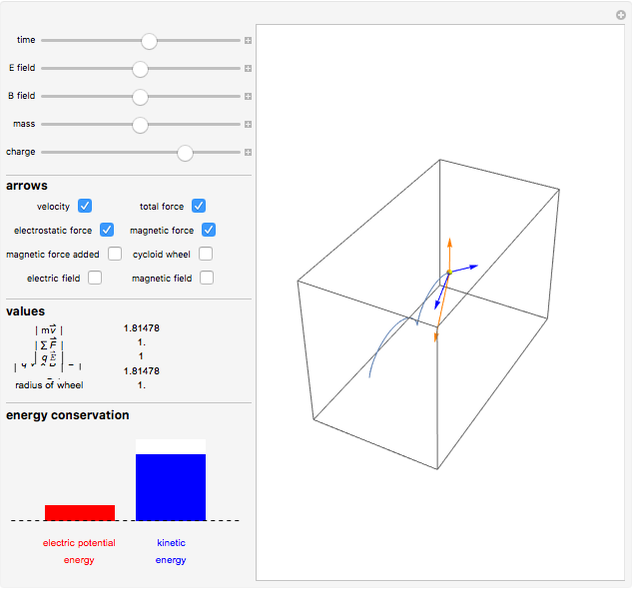
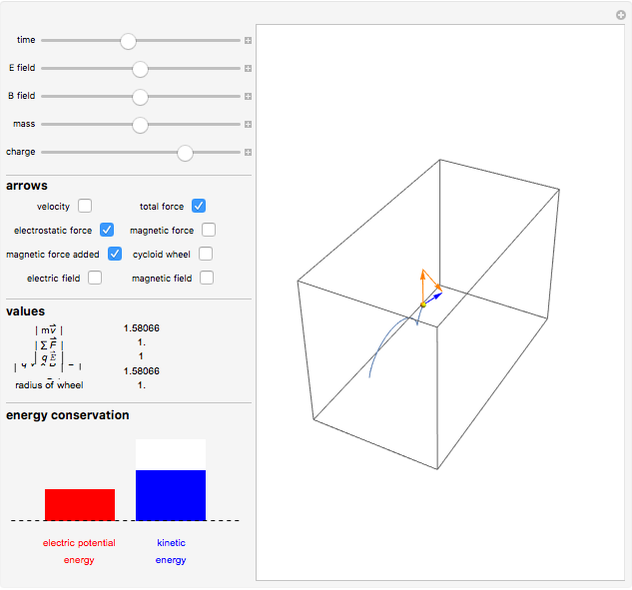
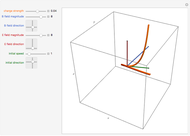
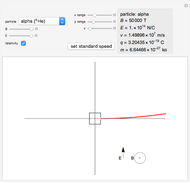
A charged particle beginning at rest in uniform perpendicular electric and magnetic fields will follow the path of a cycloid. Initially, the particle has zero speed and therefore does not experience a magnetic force. It accelerates in the direction of the electric field, its increasing velocity causing it to circle around the magnetic field lines, which are always perpendicular to its motion. The particle eventually begins to move against the electric field, decreasing its speed and eventually bringing it to rest, whereupon the entire cycle repeats itself. The sum of the particle's kinetic energy and electric potential energy (which changes linearly with the  component) remains constant throughout the process, as a consequence of energy conservation.
component) remains constant throughout the process, as a consequence of energy conservation.
Contributed by: Alexander Dalzell (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Additional details are given as comments in the code.
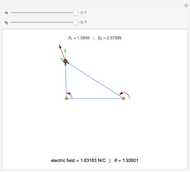
Snapshot 1: the velocity, electric force, magnetic force, and total force of the particle
Snapshot 2: the magnetic force and electric force vectors sum to the total force vector
Snapshot 3: the electric and magnetic fields are perpendicular
Snapshot 4: the motion of the particle is always perpendicular to the magnetic field
Snapshot 5: the total force always points toward the center of the cycloid wheel
Inspired by and solved in Example 5.2 of D. J. Griffiths, Introduction to Electrodynamics, 3rd ed., Upper Saddle River, NJ: Prentice Hall, 1999.