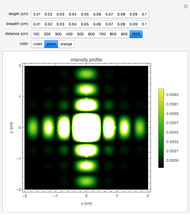
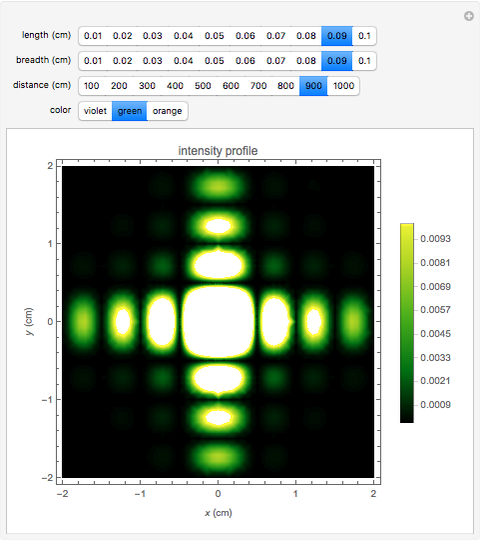
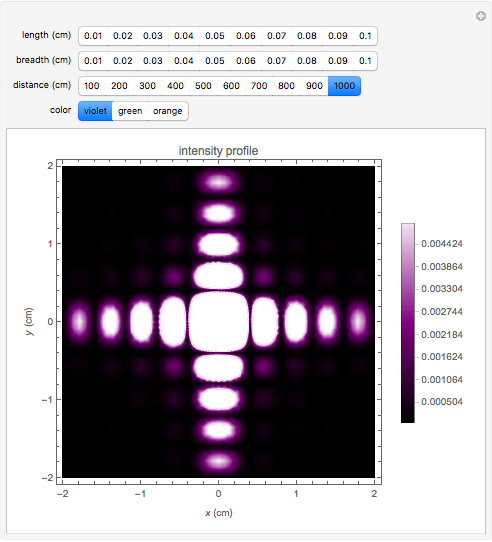
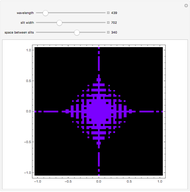
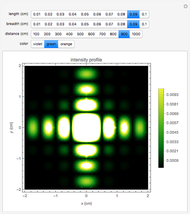
This Demonstration illustrates Fraunhofer optical diffraction through a rectangular aperture. The length and breadth determine the dimensions of the aperture in cm (length is along the horizontal axis and breadth along the vertical axis). The distance control specifies the distance between the aperture and the screen. Color is related to the wavelength of light used to illuminate the aperture. Violet corresponds to 400nm, green is around 500nm and orange is at 600nm. You can change the parameters to observe the variation in the intensity profile on the screen.