Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

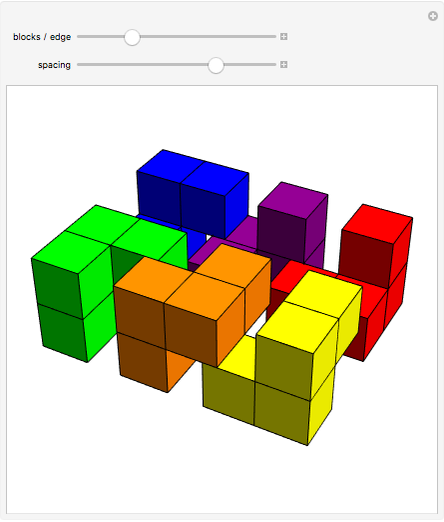
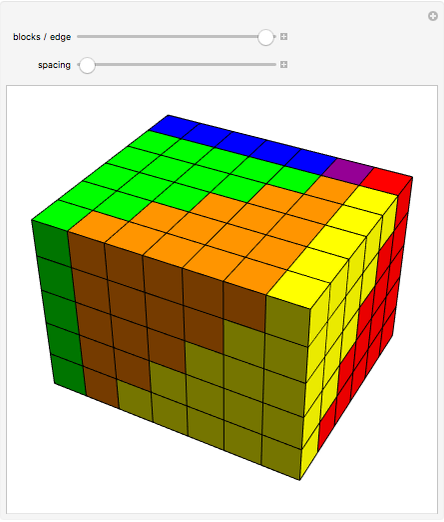
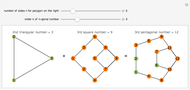
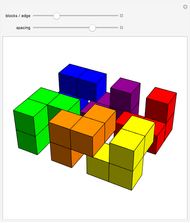
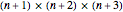Geometric Proof of the Tetrahedral Number Formula

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The tetrahedral numbers 1, 4, 10, 20, 35, are the sums of the triangular numbers,

[more]

.

This Demonstration justifies the formula by showing 6 tetrahedra with sides forming an cuboid. The controls allow you to vary the side length of the tetrahedra from 1 to 5 and to vary the spacing between them.

[less]

Contributed by: Jim Delany (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This idea was suggested by a remark in Jeffrey Stopple's A Primer of Analytic Number Theory: From Pythagoras to Riemann, New York: Cambridge University Press, 2003.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send