Keplerian Orbital Elements

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
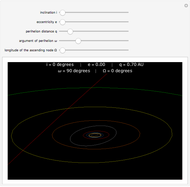
This Demonstration visualizes the influence of the Keplerian elements of a celestial body (e.g., a planet or asteroid orbiting around the Sun) on its orbit in 3-space.
Contributed by: Christoph Lhotka (January 2009)
Inspired by: Jeff Bryant
Open content licensed under CC BY-NC-SA
Snapshots
Details
Keplerian or osculating orbital elements are the natural set of variables to describe the motion of a celestial body (planet, asteroid, satellite) in 3-space: while in the 2-body problem the full set of Cartesian coordinates  changes with time, the corresponding Keplerian elements
changes with time, the corresponding Keplerian elements  are all constant except for the mean anomaly
are all constant except for the mean anomaly  . The semi-major axis
. The semi-major axis  and the eccentricity
and the eccentricity  define the form of the ellipse; the inclination
define the form of the ellipse; the inclination  , periapsis
, periapsis  , and node
, and node  define the orientation of the ellipse in 3-space. The only variable to the system is the mean anomaly
define the orientation of the ellipse in 3-space. The only variable to the system is the mean anomaly  , defining the position of the planet in its orbit.
, defining the position of the planet in its orbit.
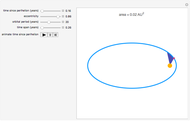
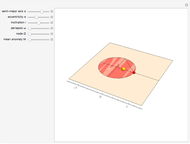
Snapshot 1: form of the ellipse (change  )
)
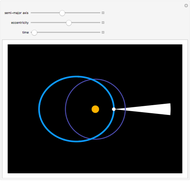
Snapshot 2: orientation of the ellipse in 3-space (change  )
)
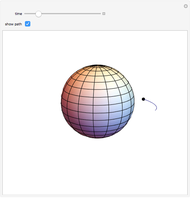
Snapshot 3: position of the body in the ellipse (change  )
)
Many more general  -body systems (solar system, lunar, or artificial satellite motion) can be modelled as perturbed two-body problems, where the Keplerian elements may oscillate around their mean values.
-body systems (solar system, lunar, or artificial satellite motion) can be modelled as perturbed two-body problems, where the Keplerian elements may oscillate around their mean values.
Permanent Citation