Looking at Polyhedra in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
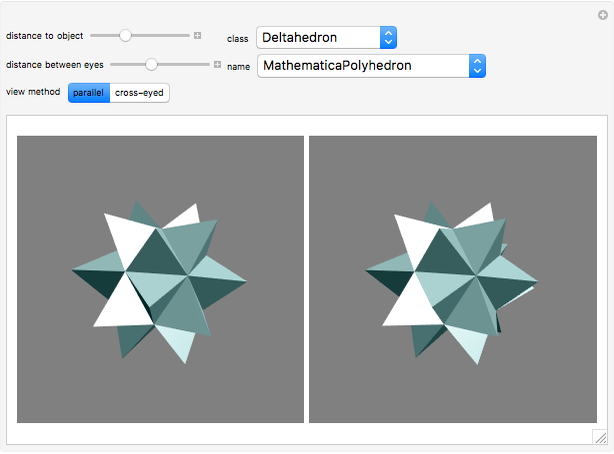
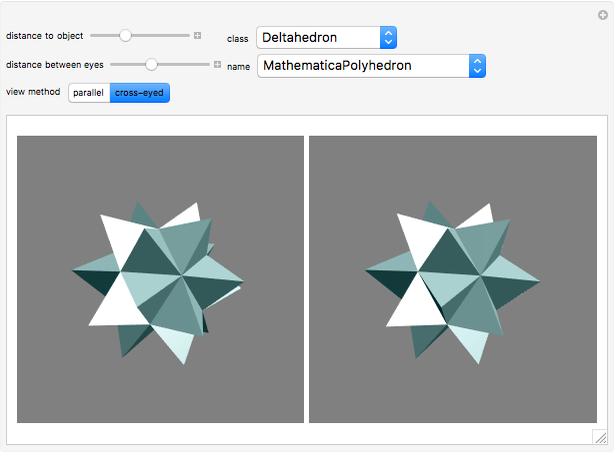
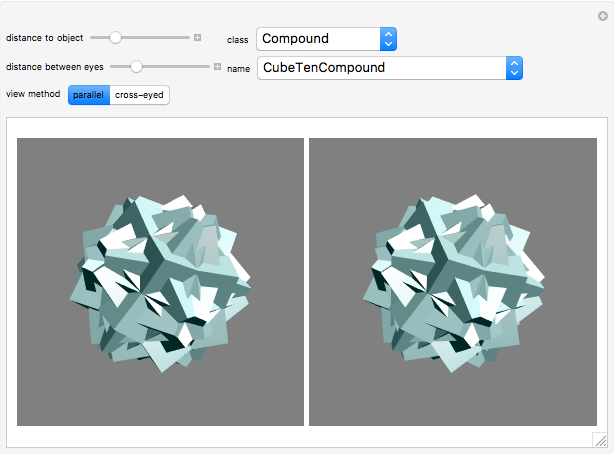
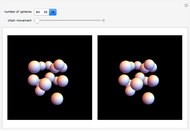
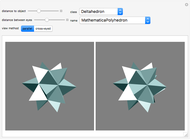
This Demonstration lets you view the polyhedra that are built into Mathematica in 3D. You can set the view method to parallel, where the left image corresponds to the left eye and the right image to the right eye, or to cross-eyed, where the images are swapped. The polyhedra are ordered by class and you can choose them from the drop-down menus. You can rotate the images by dragging them.
Contributed by: Heike Gramberg (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
When viewing an object, the image that reaches the left eye is shifted slightly relative to what the right eye sees. In stereoscopy or 3D imaging, this feature is used to create the illusion of a three-dimensional object by presenting different images to the left eye and the right eye. There are different methods to achieve this, most of which require additional equipment to view or create the images. The method used here is called freeviewing and its major advantage is that it does not need any special tools either to view or to produce the images.
In this method, the two different images are plotted side-by-side. If the left picture corresponds to the left eye and the right picture to the right eye, it is called the parallel view method. If the images are switched, it is the cross-eye view method. The observer focuses each eye on the corresponding image either by looking through the screen for parallel view or by looking cross-eyed at the screen for the cross-eyed view.
In this Demonstration the object that is being viewed can be freely rotated by dragging the shape itself. The orientation of the two images is coupled, so if the orientation of one is changed, the orientation of the other is updated automatically. The advantage of this approach (instead of using for example a 2D slider) is that the controller is located within the field of view. This helps the viewer to stay focused on the image while changing its orientation. The set of objects the viewer can choose from in this Demonstration consists of the polyhedra built into Mathematica.
Permanent Citation
"Looking at Polyhedra in 3D"
http://demonstrations.wolfram.com/LookingAtPolyhedraIn3D/
Wolfram Demonstrations Project
Published: April 13 2011