Probabilistic Interpretation of a Fractional Derivative

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
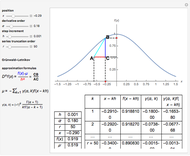
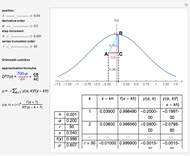
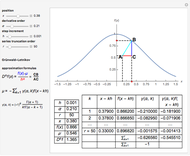
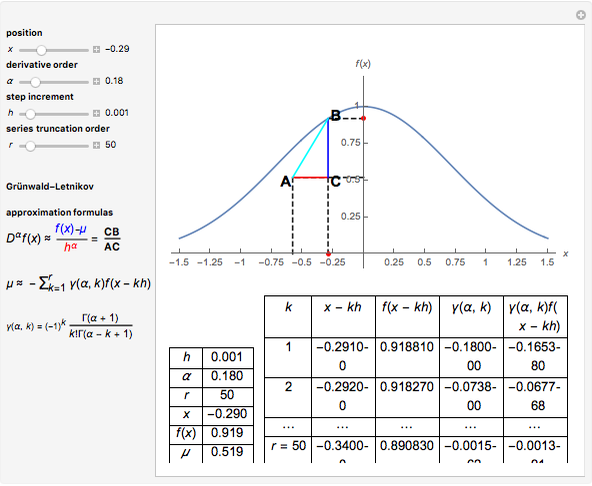
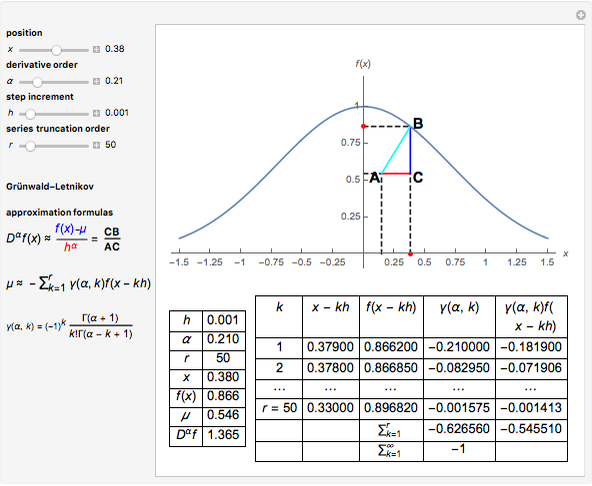
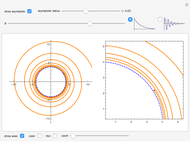
This Demonstration explores the Grünwald–Letnikov definition of the fractional derivative and its numerical approximation. A geometric and probabilistic interpretation is depicted. The displayed tabular data supports the numerical calculation.
Contributed by: L. A. Mendes Afonso and J. A. Tenreiro Machado (March 2011)
After work by: J. A. Tenreiro Machado
Open content licensed under CC BY-NC-SA
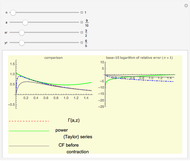
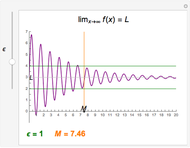
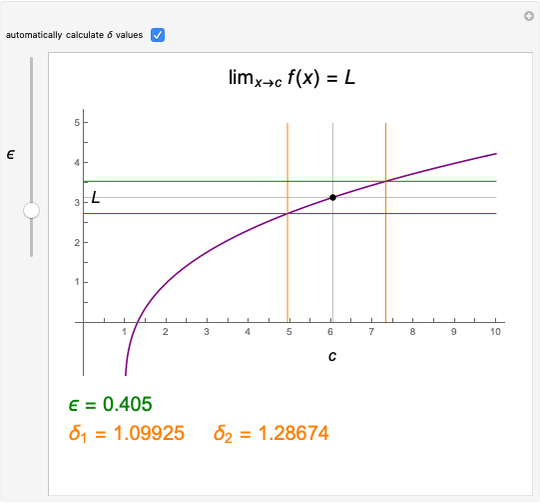
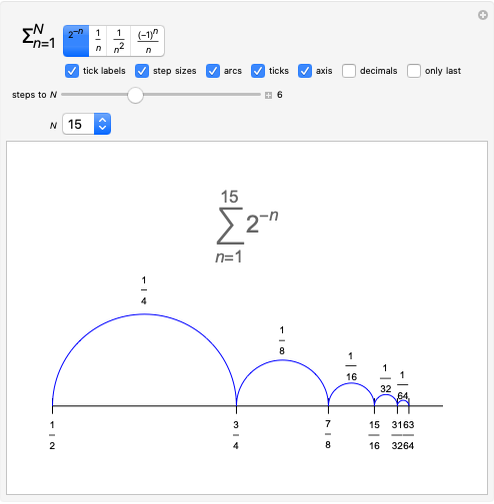
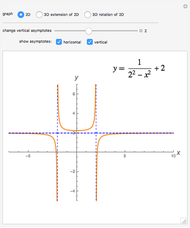
Snapshots
Details
The Grünwald–Letnikov definition of the fractional derivative of order 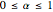 of
of  is given by the expression
is given by the expression
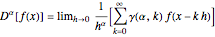 ,
,
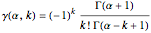 ,
,
where  represents the gamma function and
represents the gamma function and  the increment. We verify that
the increment. We verify that
 ,
,
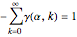 .
.
The expression  can be viewed as the expected value of the discrete random variable that for
can be viewed as the expected value of the discrete random variable that for 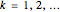 takes the value
takes the value  with probability
with probability  .
.
The Grünwald–Letnikov definition gets the slope of a triangle with upper corners  and
and 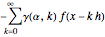 . The factor
. The factor  in the denominator expression means that, for large values of
in the denominator expression means that, for large values of  , we have a slow variation, while for small values of
, we have a slow variation, while for small values of  we have a fast variation.
we have a fast variation.
The implementation of the Grünwald–Letnikov definition of the fractional derivative corresponds to an  -term truncated series given by
-term truncated series given by
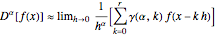 .
.
References:
[1] K. B. Oldham and J. Spanier, The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order, New York: Academic Press, 1974.
[2] I. Podlubny, Fractional Differential Equations, San Diego: Academic Press, 1999.
[3] J. A. Tenreiro Machado, "Discrete-Time Fractional-Order Controllers," Journal of Fractional Calculus & Applied Analysis, 4(1), 2001 pp. 47–66.
[4] A. A. Kilbas, H. M. Srivastava, and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Vol. 204, Amsterdam: Elsevier, 2006.
[5] J. A. Tenreiro Machado, "Fractional Derivatives: Probability Interpretation and Frequency Response of Rational Approximations," Communications in Nonlinear Science and Numerical Simulations, 14(9–10), 2009 pp. 3492–3497.
Permanent Citation