Rational Functions of Small Degree

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
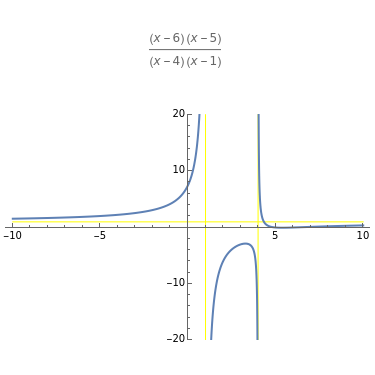
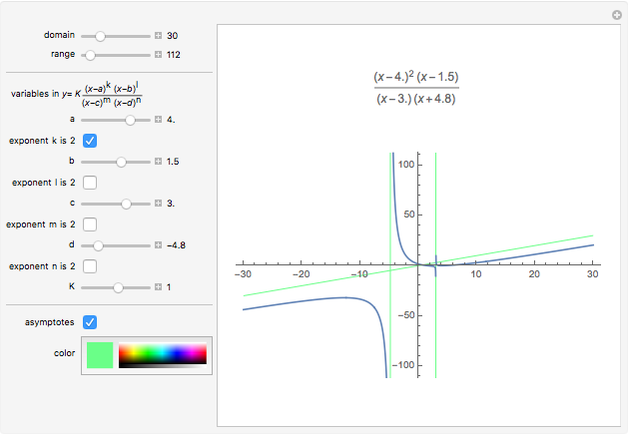
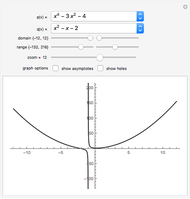
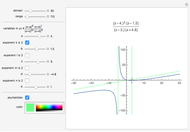
Graphing rational functions is an important topic in precalculus and calculus classes. This Demonstration illustrates the important features of the graphs of these functions, showing both vertical and horizontal asymptotes, as well as the behavior at infinity. It is limited to two roots and two vertical asymptotes, but each is allowed to be repeated. This Demonstration can be used to illustrate the difference between the behavior of a graph near single roots and double roots.
Contributed by: Donald Krug (March 2011)
Based on a program by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA
Snapshots
Details
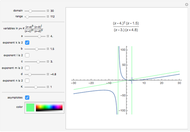
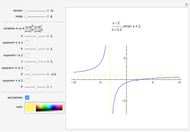
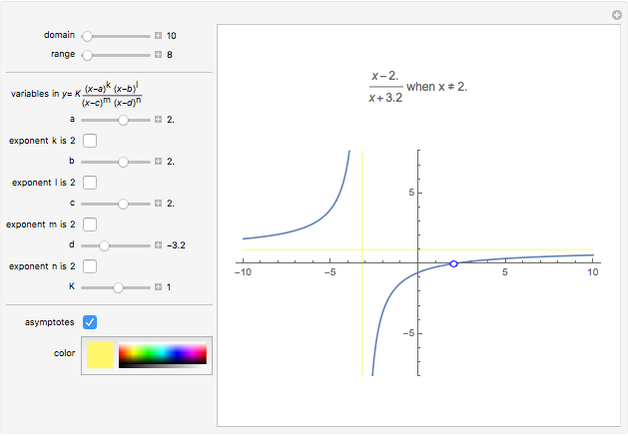
Snapshot 1: a slant asymptote
Snapshot 2: both a horizontal asymptote and where a factor in the numerator cancels a factor in the denominator
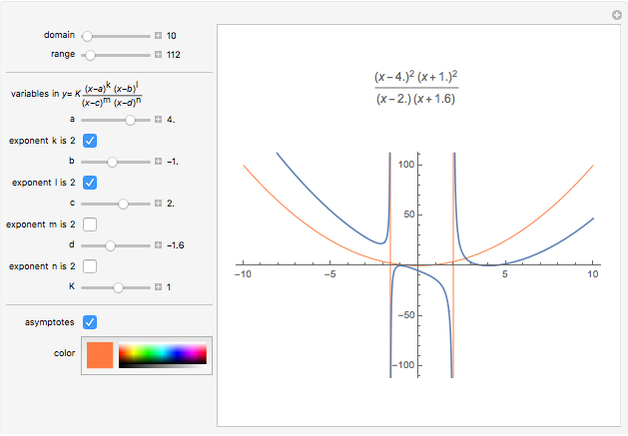
Snapshot 3: the degree of the numerator is two more than the denominator; you can highlight the endpoint behavior by increasing the domain until the red and blue graphs become superimposed, or highlight the differences for  small by reducing the size of the domain
small by reducing the size of the domain
Permanent Citation
"Rational Functions of Small Degree"
http://demonstrations.wolfram.com/RationalFunctionsOfSmallDegree/
Wolfram Demonstrations Project
Published: March 7 2011