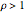Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Scalings of a GI/G/1 Queue Realization

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

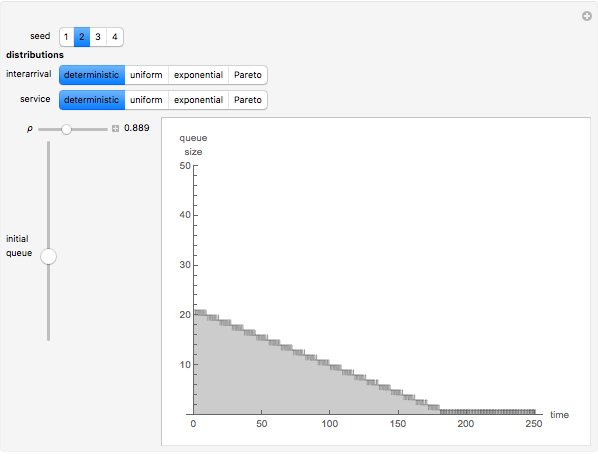
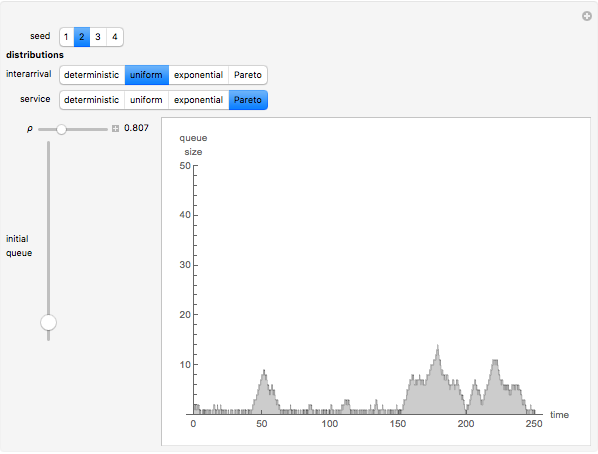
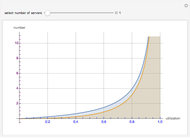
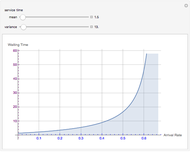
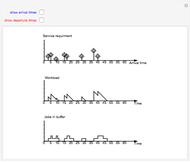
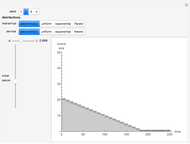
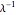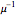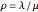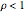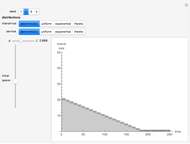
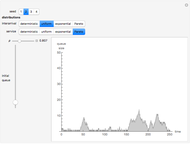
A GI/G/1 queue is a queuing system with a single server and infinite capacity. Jobs arrive according to a renewal process with a given interarrival distribution having mean and service times are i.i.d. with mean . The traffic intensity is defined as , which is a natural measure of the load on the system. It is well known that the queue length process is ergodic only if . It is also known that when 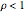, the queue length is typically larger when there is more variability in the interarrival and/or the service time distributions.

[more]

In this Demonstration we simulate the queue using interarrival and processing time sequences that are either deterministic or taken from a uniform (1/2, 3/2) distribution (which is not so variable), the more variable exponential distribution, or a very variable, heavy-tailed Pareto (1/3, 3/2) distribution that does not have a finite second moment. We then scale the processing times such that the offered load is the desired value of .

For a given sequence, you may change the initial queue conditions and the offered load and see how the queue length realization continuously changes as the time sequences are scaled. Use this to examine the behavior of the queue in the stable (), critically loaded (), and unstable () regimes.

[less]

Contributed by: Yoni Nazarathy (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send