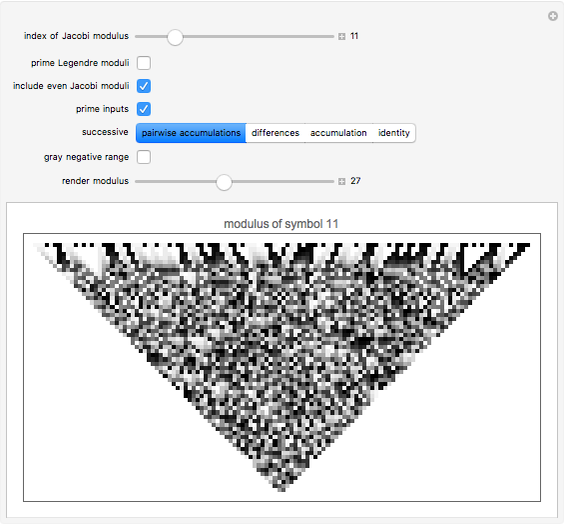
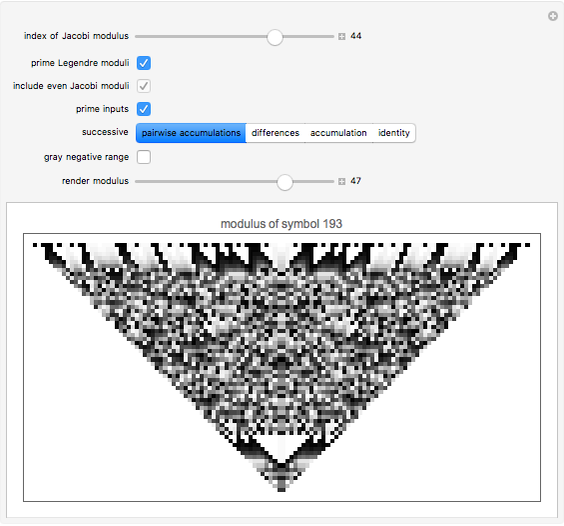
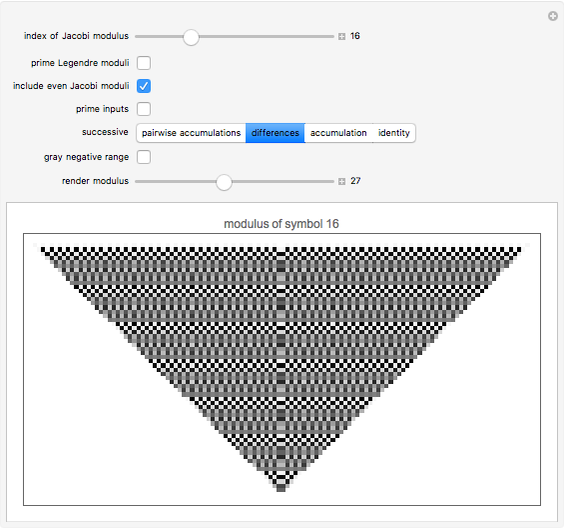
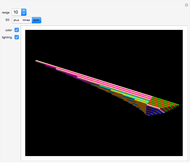
Successive Differences and Accumulations of the Jacobi Symbol

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
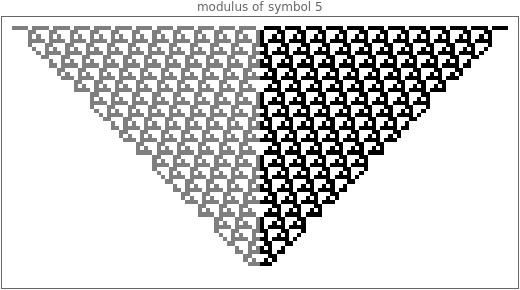
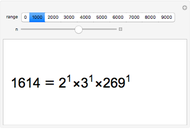
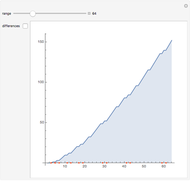
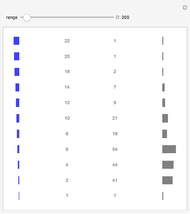
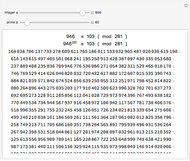
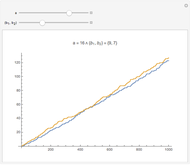
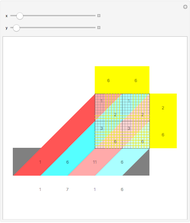
Render modular results of successive accumulations or differences for Jacobi symbols for the range -59 to 59. The Jacobi symbol extends the Legendre symbol, allowing a generalization of Gauss's celebrated quadratic reciprocity theorem.
Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A number  is called a quadratic residue modulo
is called a quadratic residue modulo 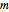 if there is a positive integer
if there is a positive integer  such that
such that 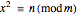 . The Jacobi symbol
. The Jacobi symbol 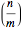 is 0 for numbers
is 0 for numbers  and
and 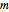 with a common factor, 1 if
with a common factor, 1 if  is a quadratic residue modulo
is a quadratic residue modulo 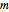 , and -1 otherwise. The Jacobi symbol reduces to the Legendre symbol if
, and -1 otherwise. The Jacobi symbol reduces to the Legendre symbol if 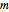 is an odd prime
is an odd prime 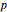 .
.
Permanent Citation