Summation by Parts

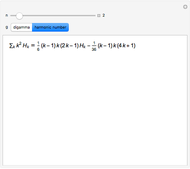
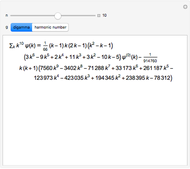
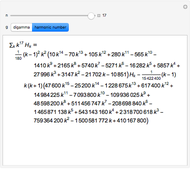
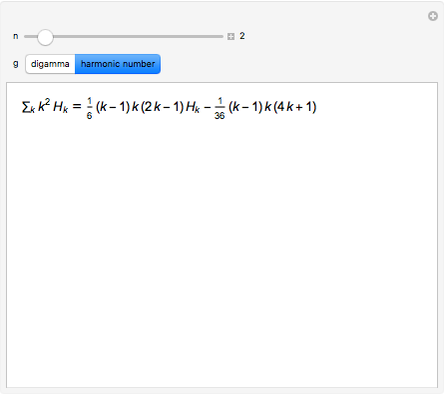
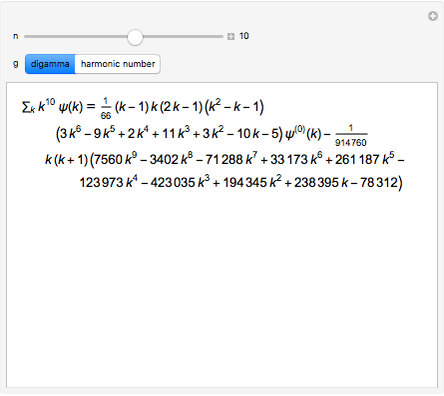
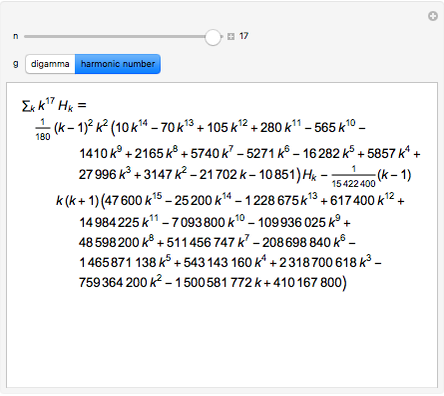
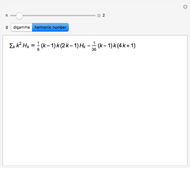
The indefinite sum of a product 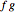can often be computed efficiently using summation by parts. For this technique to work effectively, the function must have a simple expression for its indefinite sum while 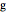must have a simple expression for its difference. Summation by parts provides a discrete analog for integration by parts that is used in ordinary infinitesimal calculus. This Demonstration considers the case when 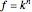is a monomial in the summation variable and 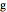is either the sequence of harmonic numbers or the digamma function, both of which have simple differences.