Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Symmetric Substitution Systems

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

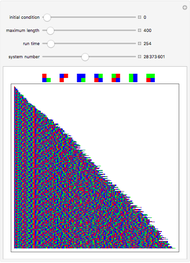
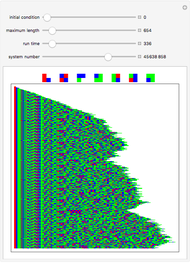
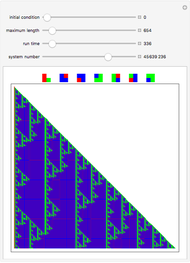
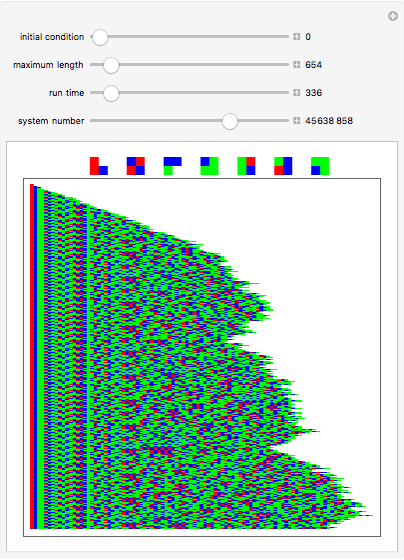
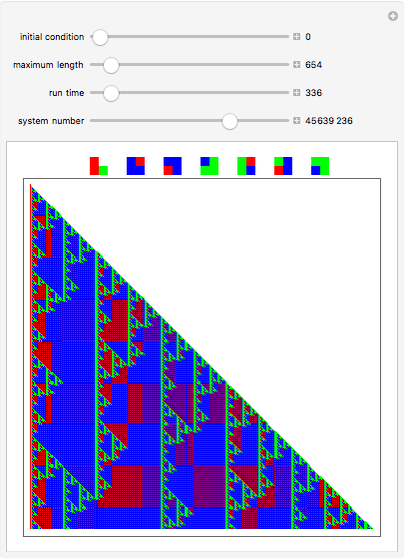
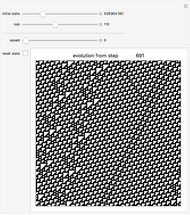
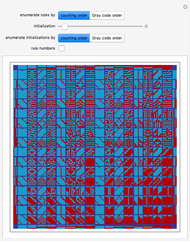
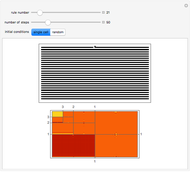
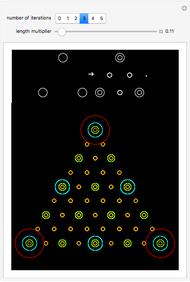
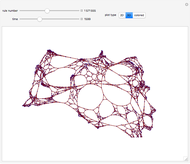
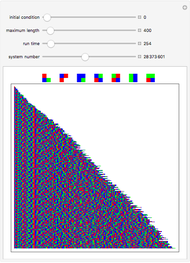
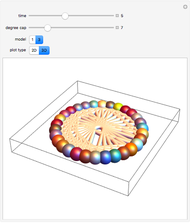
Symmetric sequential substitution systems can produce highly complex behavior from simple deterministic rules, much like cellular automata. However, symmetric sequential substitution systems can produce a wider variety of behavior because the string length can change very quickly.

[more]

This Demonstration lets you explore the fascinating space of these systems by observing space-time plots of their dynamics, where each successive row (reading down) represents the string produced upon the next time step. Each individual system is described by seven rewrite rules (shown at the top) that show which strings (above) should be replaced by which other strings (below). Unlike classic substitution systems, at each time step the string is updated by scanning it from left to right and applying the rules whenever possible in a nonoverlapping way.

[less]

Contributed by: Richard Southwell (August 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Visually exploring the behavior of these different rewrite systems is a wonderful way to study the great variety of behavior simple programs can produce. Some rules produce periodic behavior and some produce strings that grow forever (at linear or exponential rates). Still other strings fluctuate in size rapidly (growing and shrinking for many thousands of time steps).

In [1] we explore these systems in more detail and discuss many potential applications, such as arithmetic, compression, and cryptography (for reversible systems). Also see [2] for a clear discussion of these systems.

References

[1] R. Southwell and C. Cannings, "Exploring the Space of Substitution Systems," Complex Systems 22(1), 2013 pp. 1–34. www.complex-systems.com/abstracts/v22_i01_a01.html.

[2] R. Southwell. Mining the Space of Rewrite Systems [Video]. (Aug 15, 2013) www.youtube.com/watch?v=JbseluMTfZQ.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send