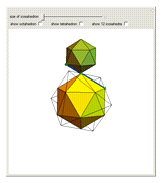
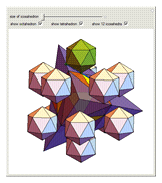
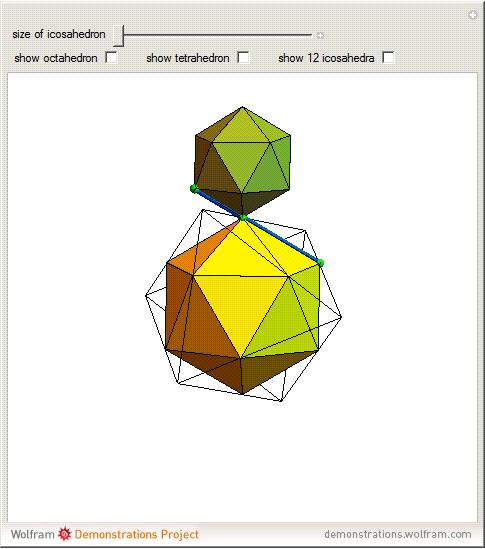
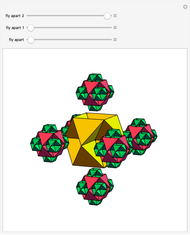
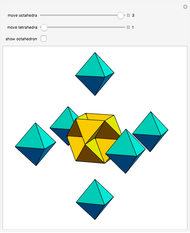
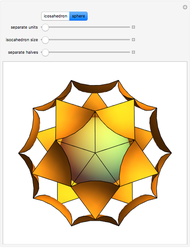
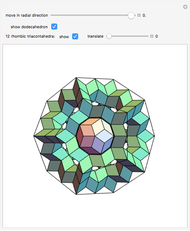
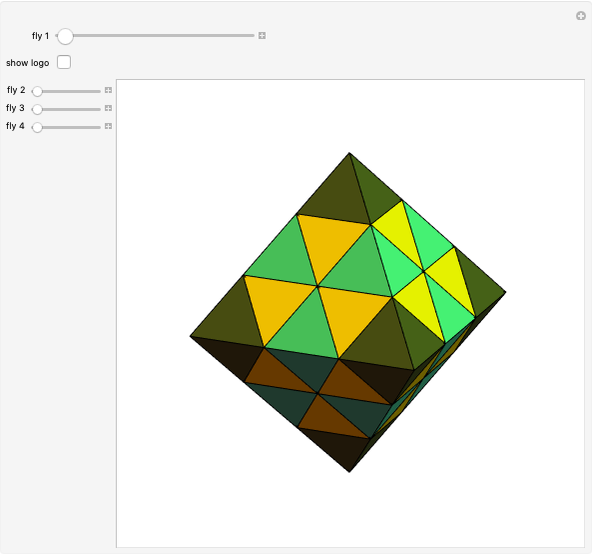
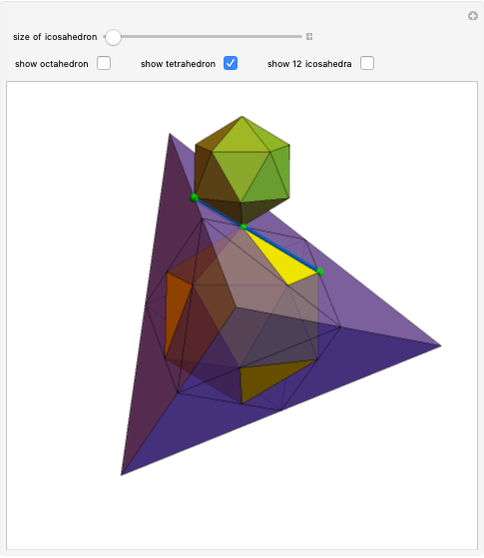
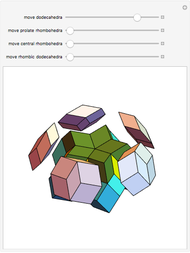
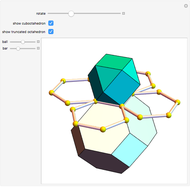
A regular octahedron 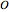is placed within a regular icosahedron 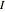so that eight of its 20 faces lie in the faces of 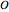. 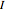, in turn, is contained within a regular tetrahedron 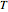whose four faces contain four of the eight faces of . The vertices of 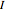divide the edges of 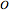in the golden ratio . If an edge of is extended in the ratio 1:, then its endpoint is on the edge of that divides it in the golden ratio.