Velocity for an Airplane to Achieve Liftoff

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
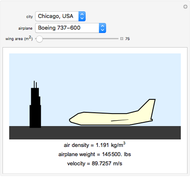
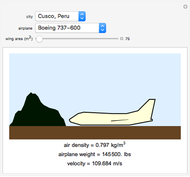
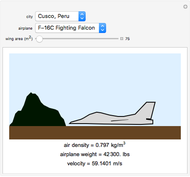
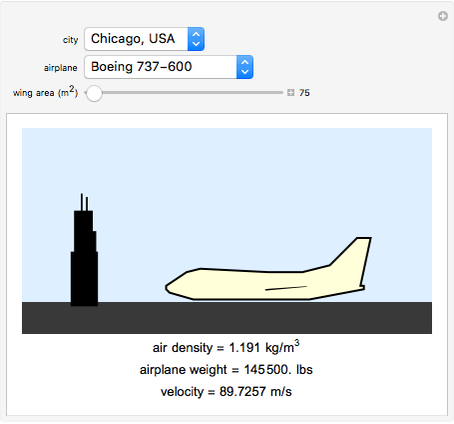
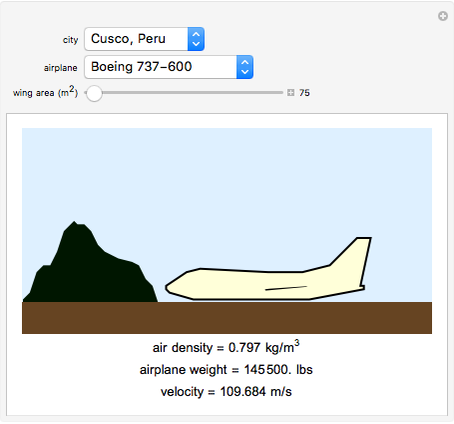
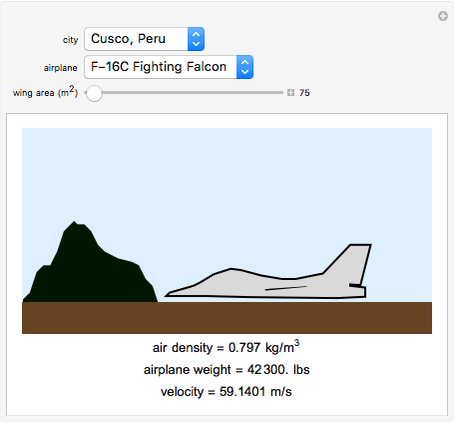
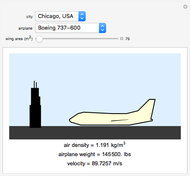
In order for an airplane to achieve lift off, the force of lift must be greater than that of its weight and the drag of the air (neglected). In this Demonstration, you can change the type of airplane, wing area, and city the airplane is in to see the necessary velocity the airplane must reach in order to lift off. The change of airplane affects the weight of the airplane and coefficient of lift, and the change of city affects the air density. These three factors and the wing area are used in computing the velocity an airplane needs in order to achieve lift off. See how the variables correlate with lift off velocity.
Contributed by: Jennifer Brand and Allison Leczycki (June 2016)
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School and Mr. Christopher Grattoni.
Based on a program by: Mark Peterson
Open content licensed under CC BY-NC-SA
Snapshots
Details
Lift can be calculated using the equation 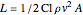 , where
, where 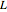 is the force of the lift,
is the force of the lift, 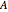 is the wing area (
is the wing area (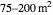 ),
),  is the air density,
is the air density, 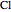 is the coefficient of lift, and
is the coefficient of lift, and  is velocity.
is velocity.
The force of lift is equivalent to the weight of the aircraft when at equilibrium in a fluid. Therefore, as long as the lift is greater than the weight of the aircraft, the aircraft ascends. The drop-down menu of the different airplanes determines the weight and the coefficient of lift.
The air density depends on the chosen city. Each city corresponds to an air density that was calculated using weather data on May 22, 2016, 12:00 EST.
Choose the inputs to see the velocity.
This Demonstration does not take into account the effects of drag.
References
[1] OpenWeatherMap, Inc. "OpenWeatherMap." (Jun 8, 2016) www.openweathermap.org/city/2643743.
[2] Barani Design. "Air Density Calculator." (Jun 8, 2016) barani.biz/apps/air-density.
[3] United States Board on Geographic Names. "Geographic Names Information System." (Jun 8, 2016) http://geonames.usgs.gov/apex/f?p=136:1:0:::::.
[5] T. Benson (ed.). "Lift Formula." (Jun 8, 2016) www.grc.nasa.gov/www/k-12/WindTunnel/Activities/lift_formula.html.
[6] J. Roskam, Airplane Design Part I: Preliminary Sizing of Airplanes, Lawrence: Kansas: DARcorporation, 2015.
Permanent Citation
"Velocity for an Airplane to Achieve Liftoff"
http://demonstrations.wolfram.com/VelocityForAnAirplaneToAchieveLiftoff/
Wolfram Demonstrations Project
Published: June 9 2016