Wheels on Wheels on Wheels

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
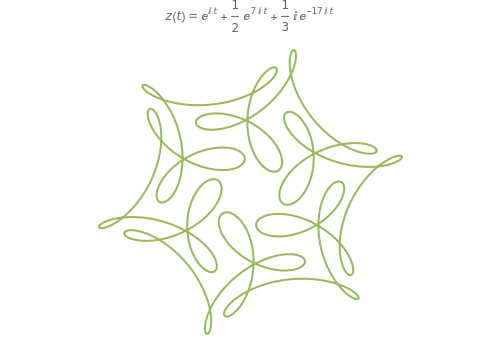
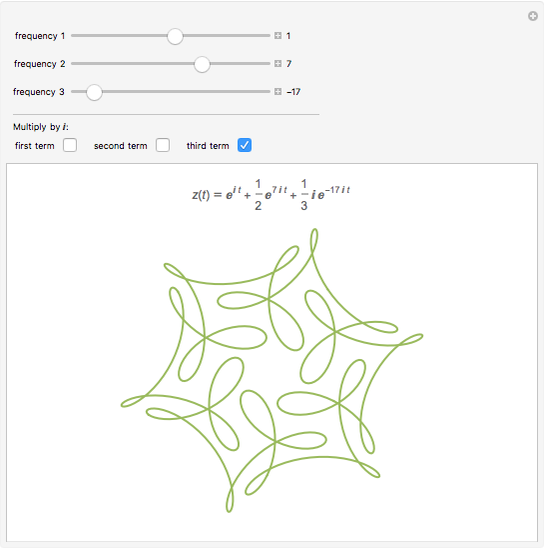
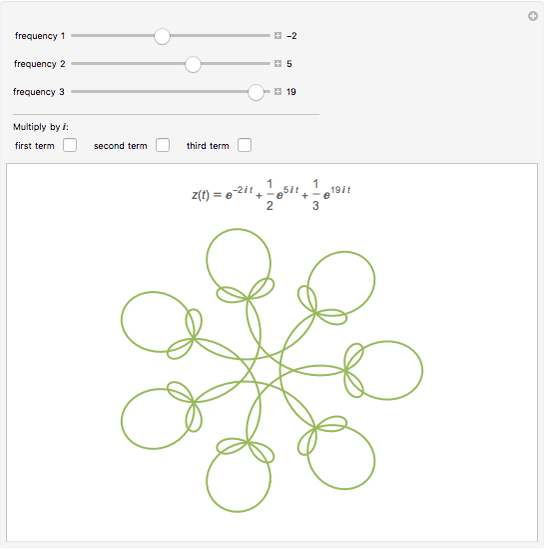
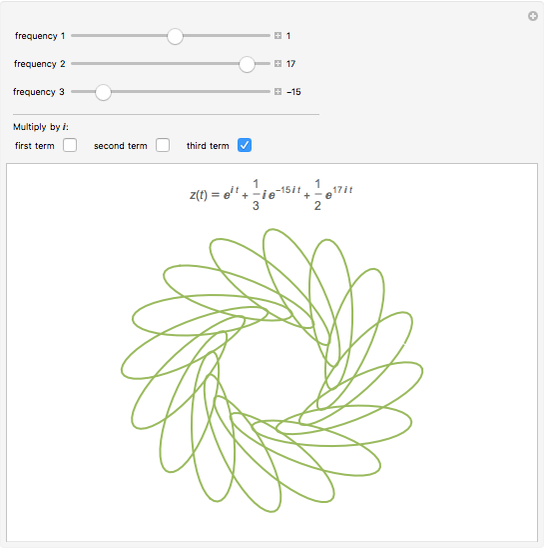
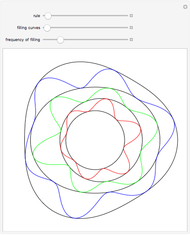
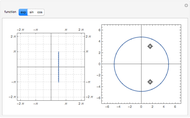
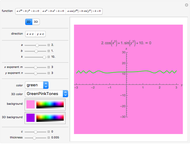
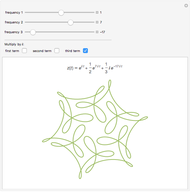
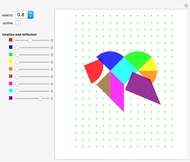
Consider a wheel of radius 1 rotating about its axis with a frequency of 1 turn per second. Now imagine that there is a second, smaller wheel, the center of which is attached to a point on the circumference of the first. This second wheel is rotating on its own axis at a frequency of 7 turns per second. Finally, imagine a third, yet smaller wheel, whose center is attached to a point on the circumference of the second. This third wheel is also rotating on its own axis but in the other direction to the other two and at a frequency of 15 turns per second. A pencil put on the circumference of this third wheel would trace out a closed pattern of loops with two-fold symmetry.
[more]
Contributed by: Michael Croucher (March 2011)
After work by: Daniel de Souza Carvalho
Open content licensed under CC BY-NC-SA
Snapshots
Details
It was shown in a paper by Farris that the resulting curve exhibits 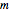 -fold symmetry if the three frequencies are congruent (mod
-fold symmetry if the three frequencies are congruent (mod 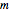 ).
).
Reference: F. A. Farris, "Wheels on Wheels on Wheels—Surprising Symmetry," Mathematics Magazine 69(3), 1996 pp. 185–189.
Permanent Citation