A Visual Proof of Ptolemy's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
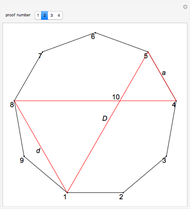
A significant result in classical geometry is Ptolemy's theorem: in a cyclic quadrilateral, the sum of the products of the two pairs of opposite sides is equal to the product of the diagonals. This Demonstration presents a visual proof of the theorem, based on [1].
[more]
Contributed by: Tomas Garza (April 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
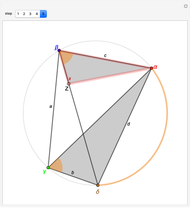
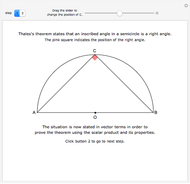
1. The four vertices of a quadrilateral  with vertices
with vertices  ,
,  ,
,  ,
,  all lie on the circumference of a circle.The lengths of the sides of
all lie on the circumference of a circle.The lengths of the sides of  are
are  ,
,  ,
,  ,
,  and the lengths of its diagonals are
and the lengths of its diagonals are  and
and  .
.
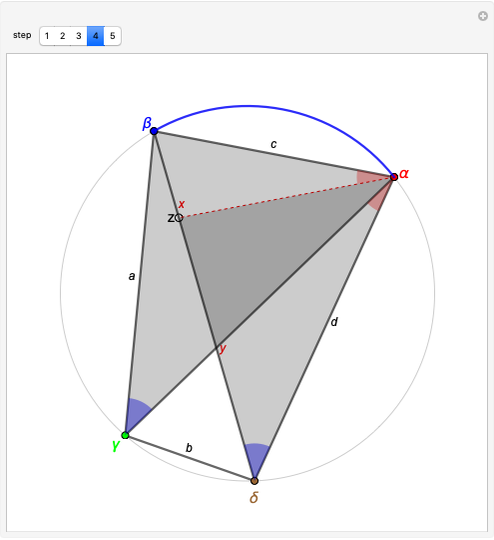
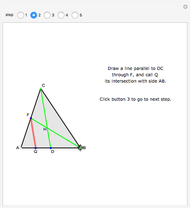
2. Draw the line  (dashed red) so that
(dashed red) so that 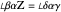 , where
, where  is on the diagonal
is on the diagonal  . That is, the two red angles are equal. Let
. That is, the two red angles are equal. Let  and
and  , so that
, so that  .
.
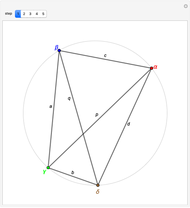
3. The two blue angles are equal since they subtend the same blue arc from  to
to  . Hence, the two triangles
. Hence, the two triangles  and
and  are similar, since they have two equal angles, the blue ones and the red angles plus
are similar, since they have two equal angles, the blue ones and the red angles plus  .
.
4. Since the two shaded triangles are similar,
 ,
,
or  .
.
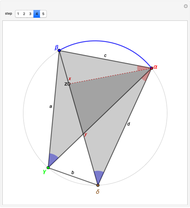
5. The two orange angles are equal,  , since they subtend the same arc
, since they subtend the same arc  . The triangle
. The triangle  (with pink sides) and the triangle
(with pink sides) and the triangle  (with dark blue sides) are similar since the two angles
(with dark blue sides) are similar since the two angles  and
and  at vertex
at vertex  are equal from step 2. Then
are equal from step 2. Then
 ,
,
or  .
.
Finally, adding the two results,
 .
.
Reference
[1] C. Alsina and R. B. Nelsen, When Less Is More: Visualizing Basic Inequalities, Washington, D.C.: Mathematical Association of America, 2009 p. 112. doi:10.5948/UPO9781614442028.
Permanent Citation