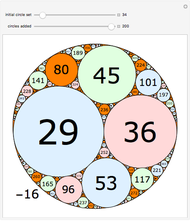
Apollonian Edge Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
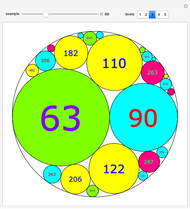
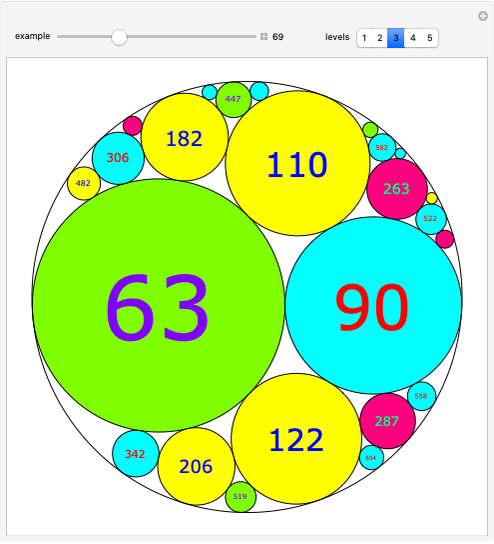
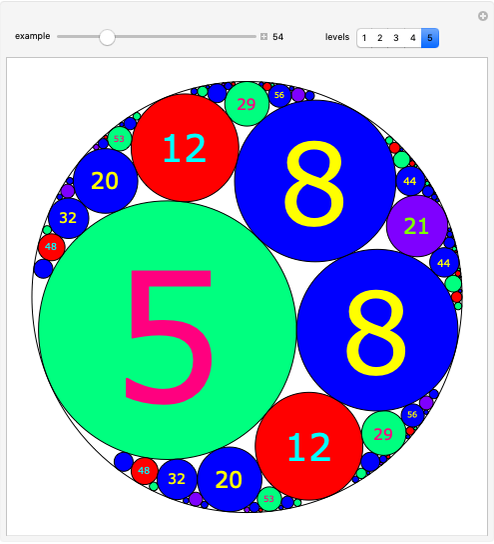
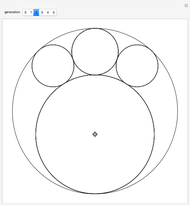
The curvature (or bend) of a circle of radius  is
is  .
.
Contributed by: Ed Pegg Jr (April 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] E. Pegg Jr. "The Circles of Descartes" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheCirclesOfDescartes.
[2] OEIS, A004613, Numbers that are divisible only by primes congruent to 1 mod 4.
[3] J. C. Lagarias, C. L. Mallows and A. R. Wilks, "Beyond the Descartes Circle Theorem." arxiv.org/abs/math/0101066.
[4] D. Austin. "When Kissing Involves Trigonometry." American Mathematical Society, March 2006. www.ams.org/featurecolumn/archive/kissing.html.
Permanent Citation