Base Conversions from Base 2 through 100 Using Radix Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
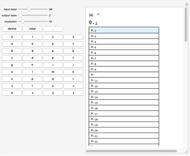
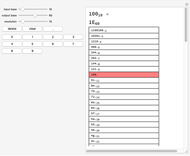
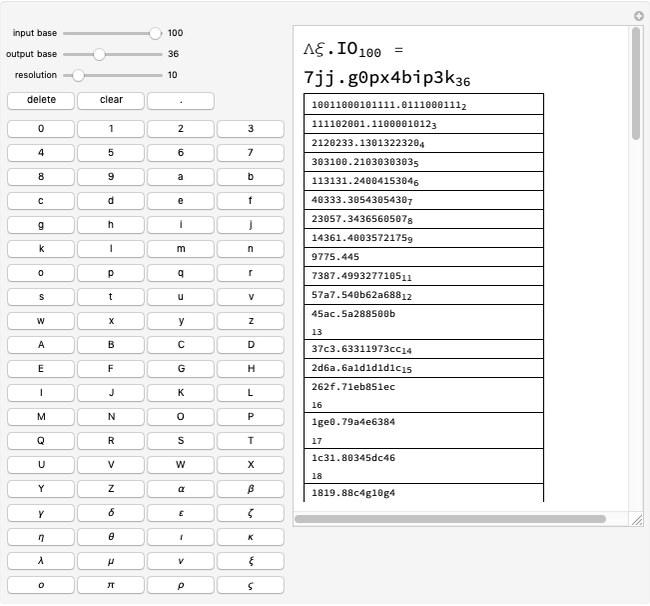
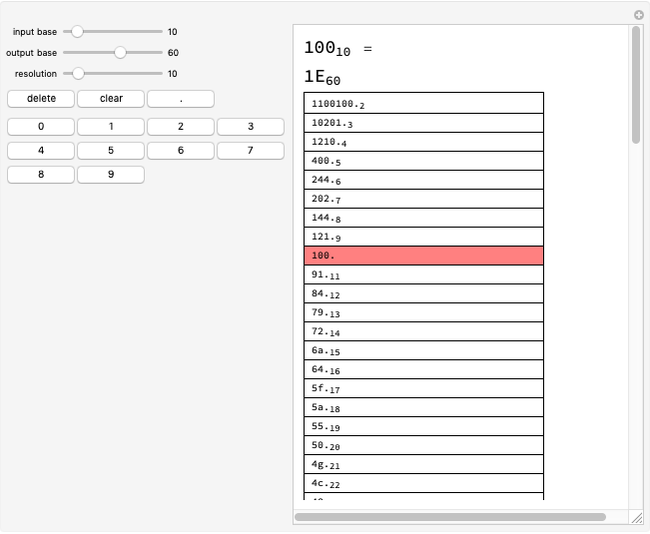
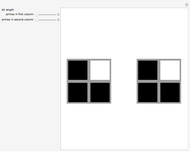
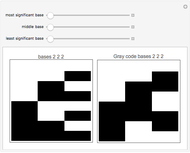
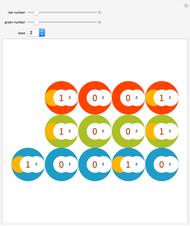
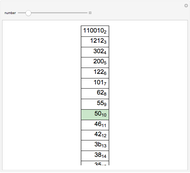
This Demonstration converts a given number in some base from 2 to 100 into all bases from 2 to 100.
[more]
Contributed by: Shreyas Poyrekar and Aaron T. Becker (February 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
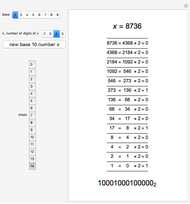
A number written in a base form can be converted into any other base form. In this Demonstration, the number is first converted into base 10, and the resulting decimal number is converted into the required base form.
Given an integer in base  , the decimal value is obtained by multiplying the
, the decimal value is obtained by multiplying the 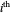 digit by
digit by 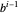 and summing the result. Digits to the left of the radix point are multiplied by
and summing the result. Digits to the left of the radix point are multiplied by  to increasing powers, starting at
to increasing powers, starting at 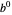 . Digits to the right of the radix are multiplied by decreasing powers of
. Digits to the right of the radix are multiplied by decreasing powers of  .
.
For example:
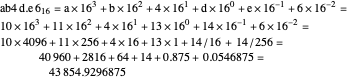
To convert a decimal number to base  , let
, let 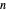 be the integer part of the decimal number and
be the integer part of the decimal number and 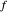 be the fractional part.
be the fractional part.
First compute the integer part. Divide 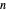 by
by  ; the remainder is the least significant digit of the integer. The process repeats: divide the quotient by
; the remainder is the least significant digit of the integer. The process repeats: divide the quotient by  , and use the remainder as the next most significant digit of the integer part. The process terminates when the quotient is 0, and the last remainder is the most significant digit.
, and use the remainder as the next most significant digit of the integer part. The process terminates when the quotient is 0, and the last remainder is the most significant digit.
Next, compute the fractional part. Let 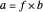 ;
;  is always less than
is always less than 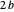 . The integer part of
. The integer part of 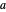 is the next digit to the right of the radix point of the number in base
is the next digit to the right of the radix point of the number in base  . This digit may be zero.
. This digit may be zero.
Continue multiplying the fractional part of 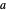 by
by  until the fractional part is zero or a sufficient resolution is reached.
until the fractional part is zero or a sufficient resolution is reached.
For example, 0.44 to base 6:
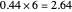 , giving the answer to one digit precision of
, giving the answer to one digit precision of 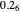
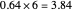 , giving the answer to two digit precision of
, giving the answer to two digit precision of 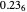
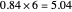 , giving the answer to three digit precision of
, giving the answer to three digit precision of 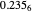
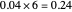 , giving the answer to four digit precision of
, giving the answer to four digit precision of 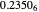
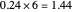 , giving the answer to five digit precision of
, giving the answer to five digit precision of 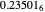
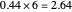 , giving the answer to six digit precision of
, giving the answer to six digit precision of 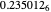
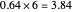 , giving the answer to seven digit precision of
, giving the answer to seven digit precision of 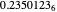
...
The remainder repeats: 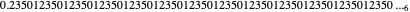 .
.
References
[1] Wikipedia. "Radix." (Feb 20, 2020) en.wikipedia.org/wiki/Radix.
[2] Wikipedia. "Numeral System". (Feb 20 2020) en.wikipedia.org/wiki/Numeral_system.
Permanent Citation