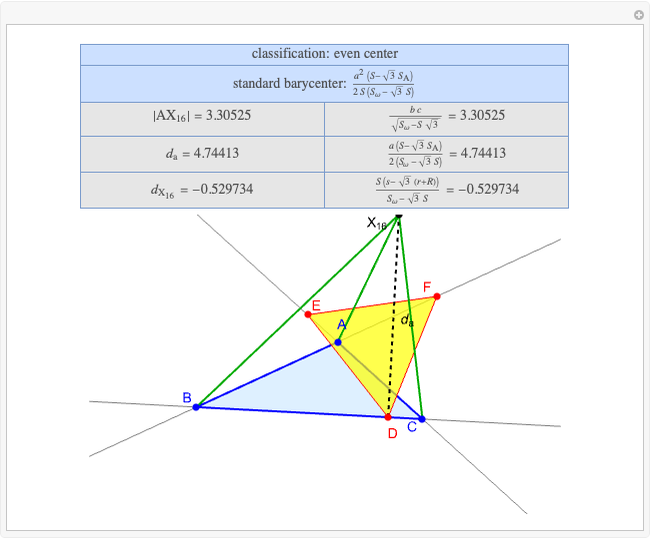
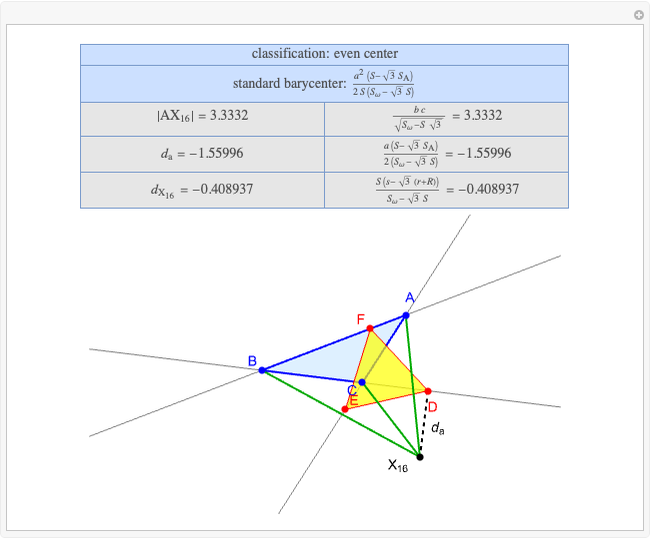
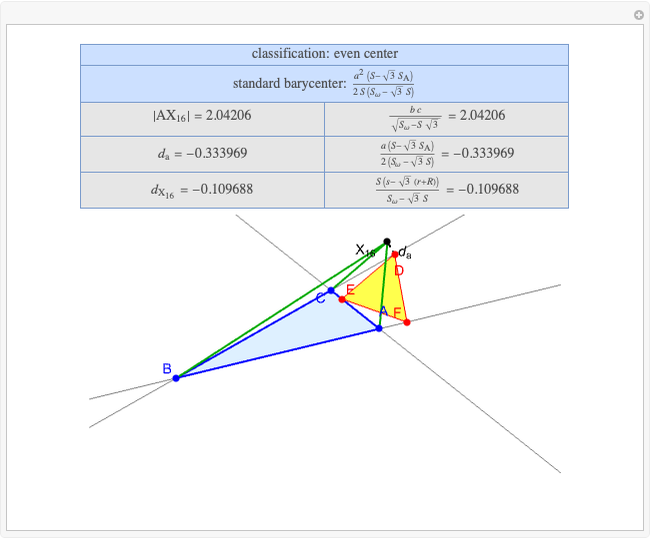
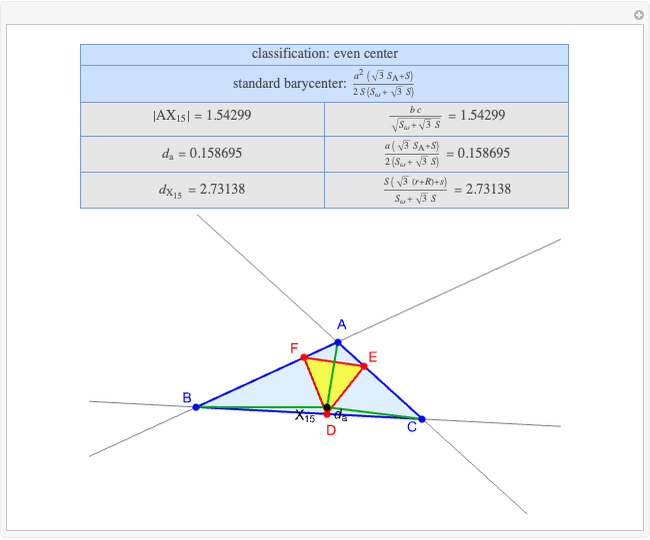
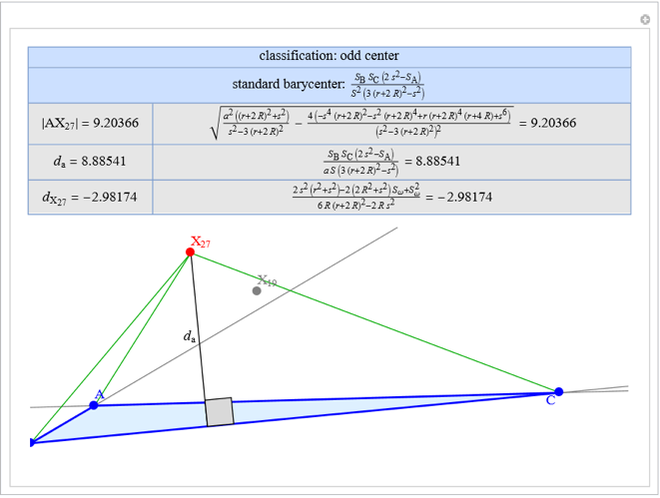
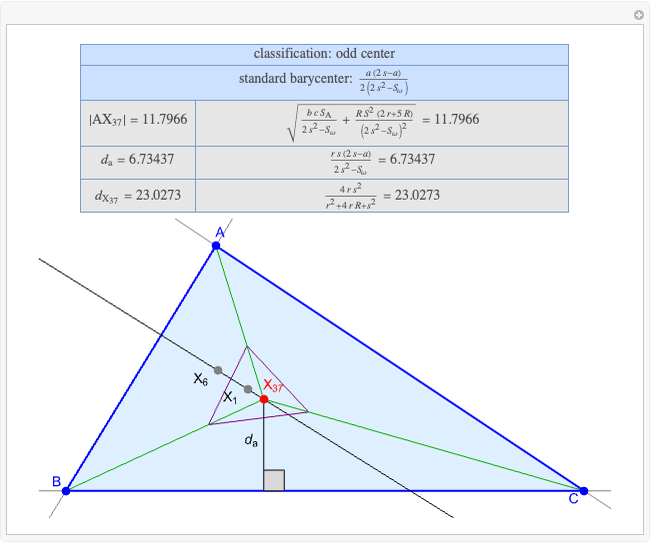
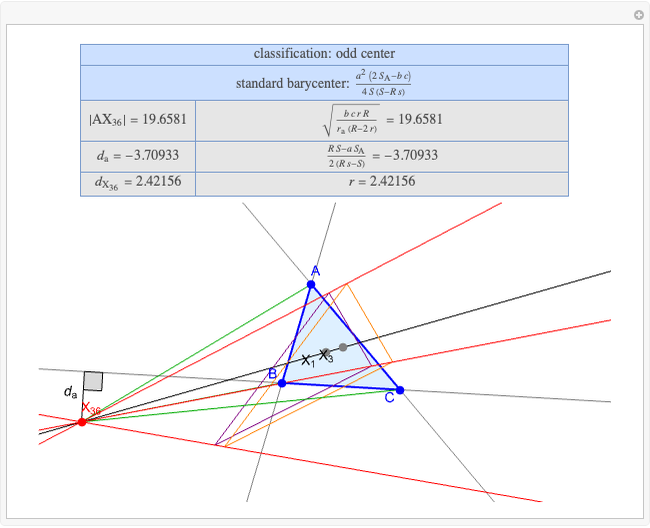
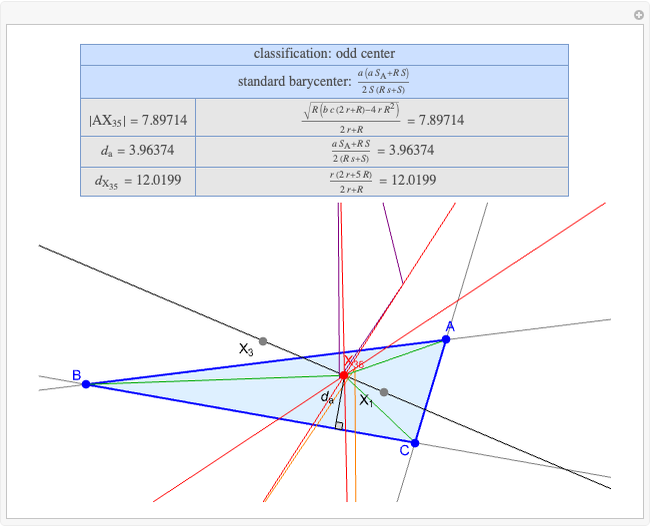
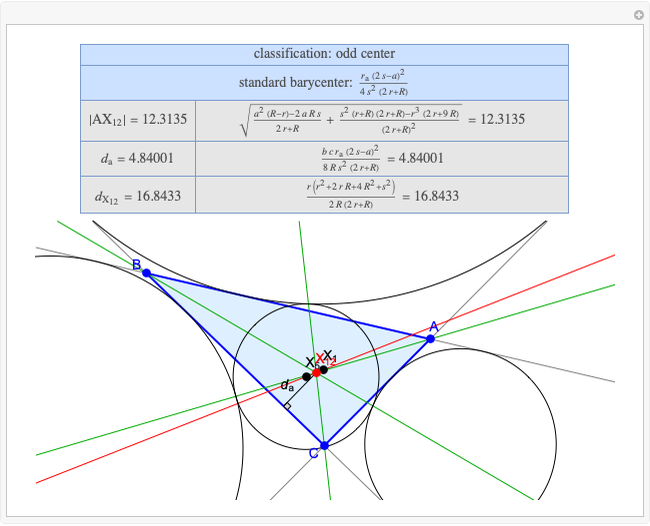
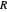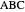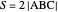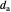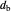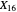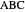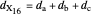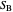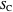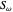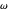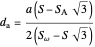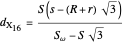Basic Parameters of the Second Isodynamic Point

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A triangle 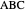 has two isodynamic points, defined by the property that their pedal triangles are equilateral. The second isodynamic point
has two isodynamic points, defined by the property that their pedal triangles are equilateral. The second isodynamic point 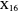 is the isogonal conjugate of the second Fermat point [1].
is the isogonal conjugate of the second Fermat point [1].
Contributed by: Minh Trinh Xuan (January 2023)
Open content licensed under CC BY-NC-SA
Snapshots
Details
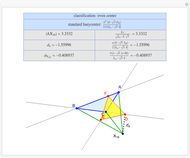
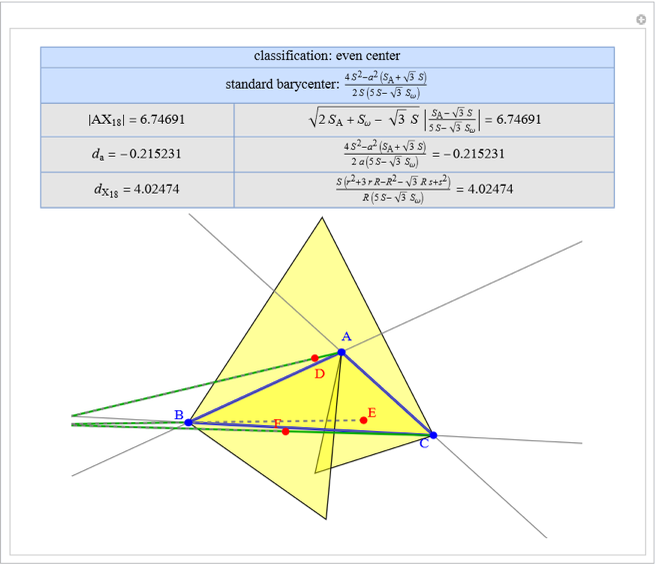
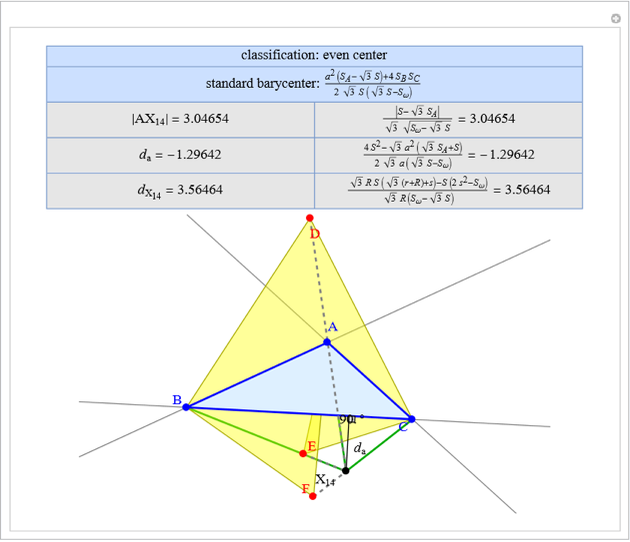
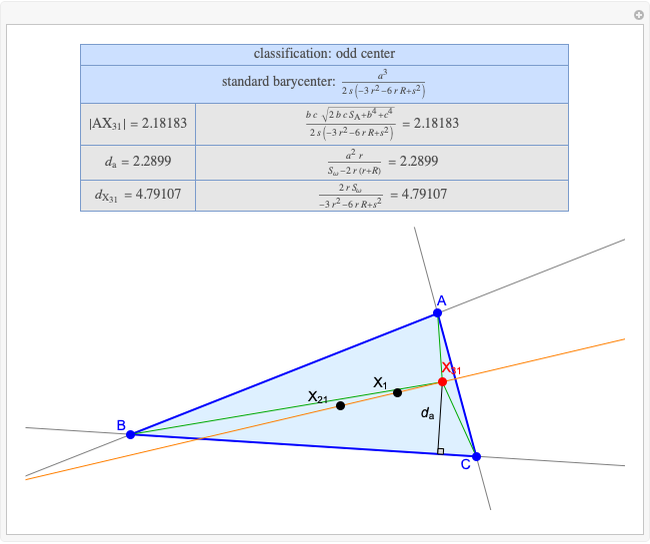
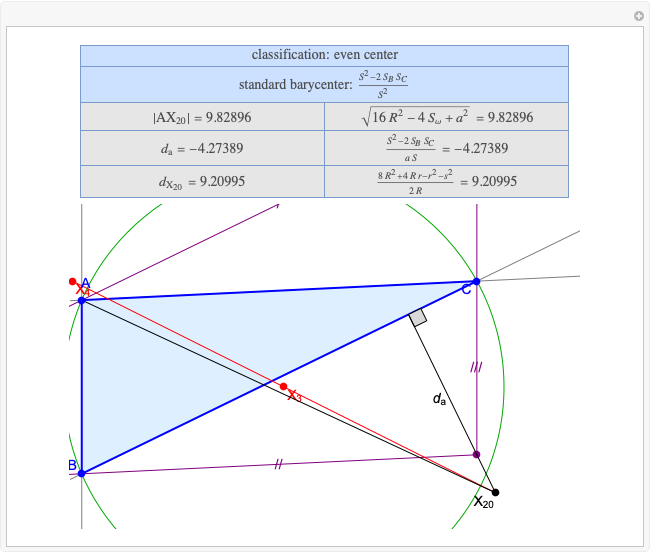
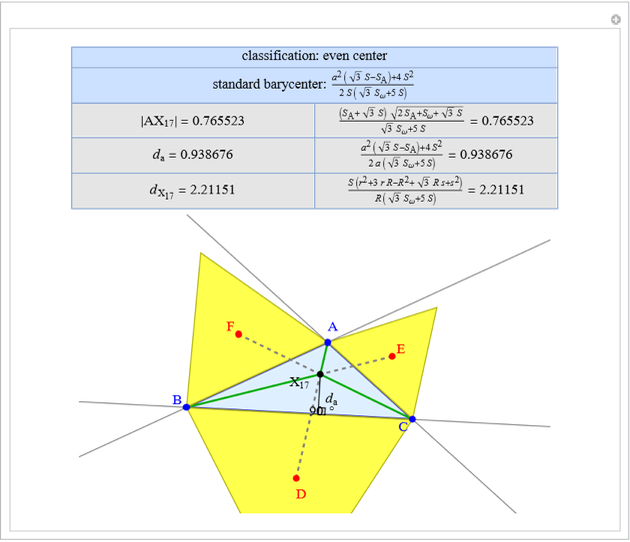
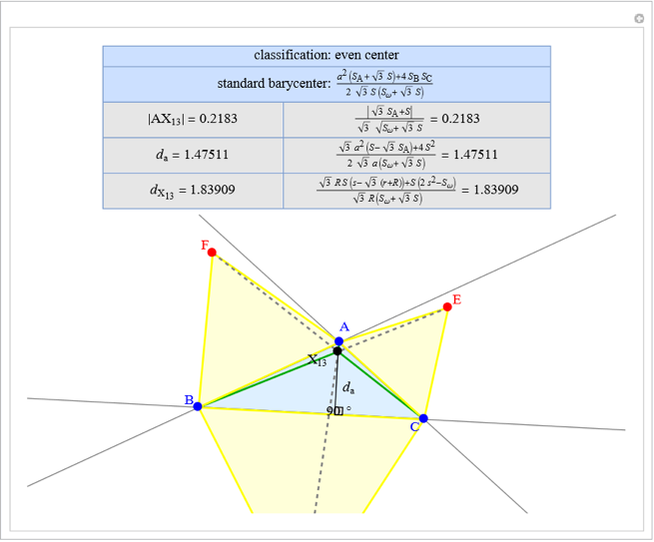
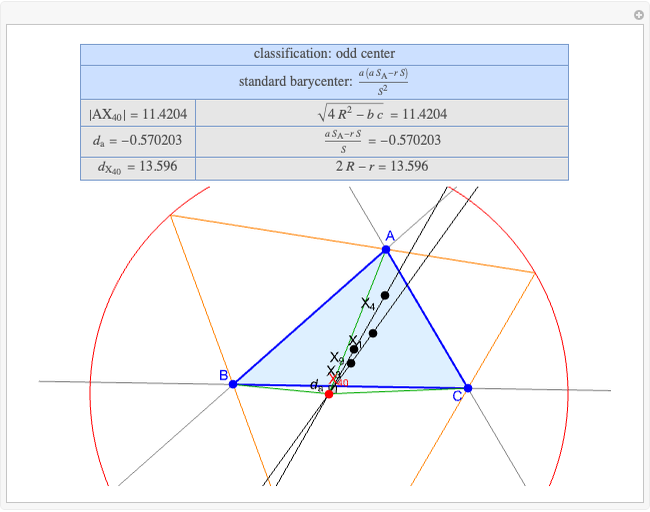
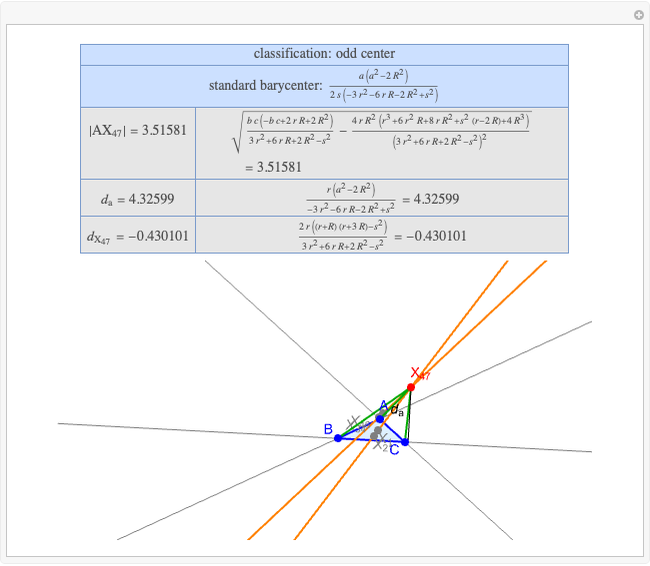
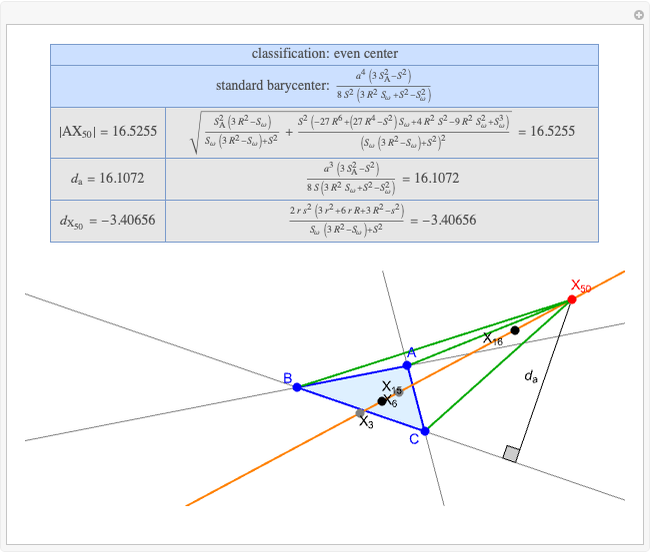
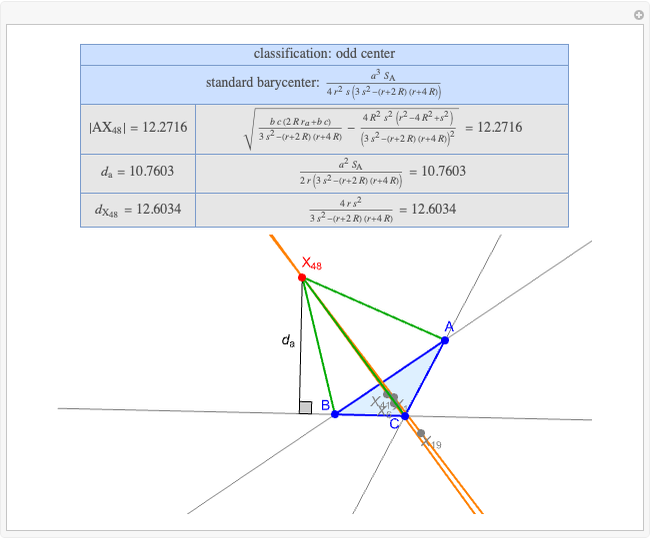
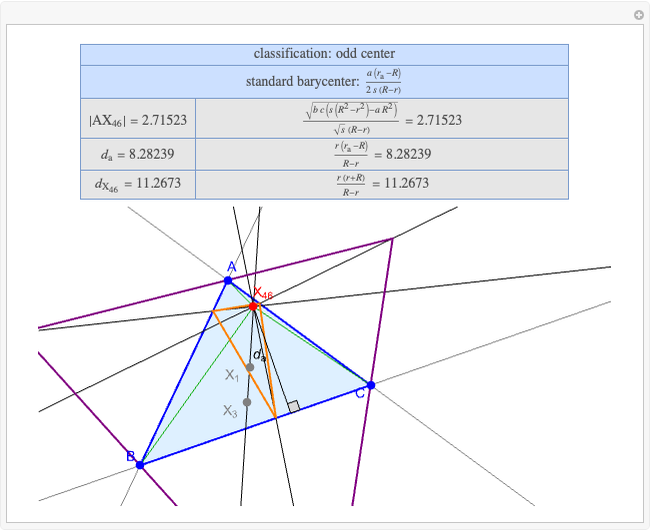
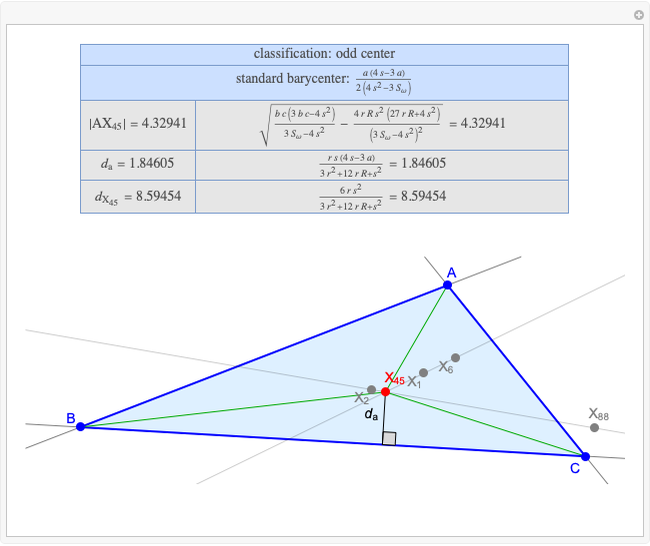
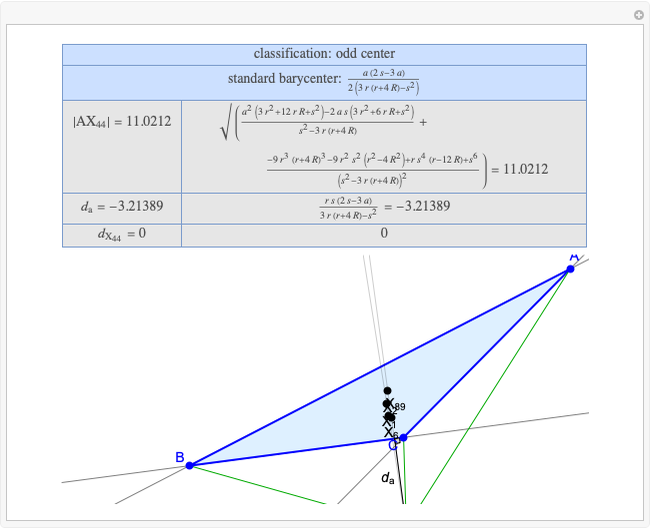
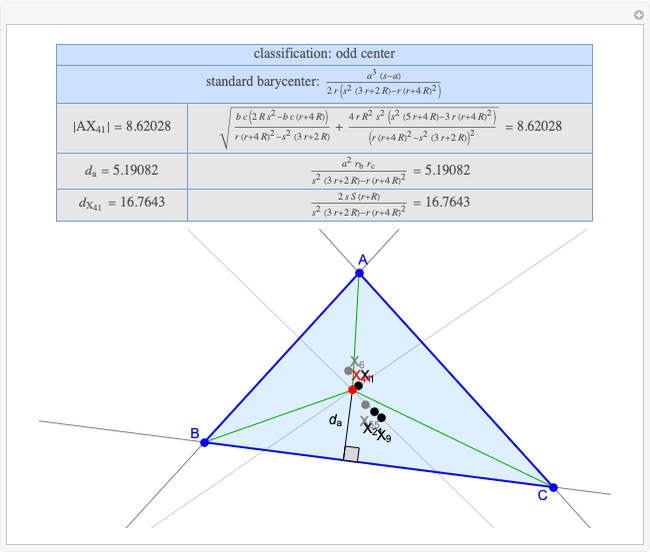
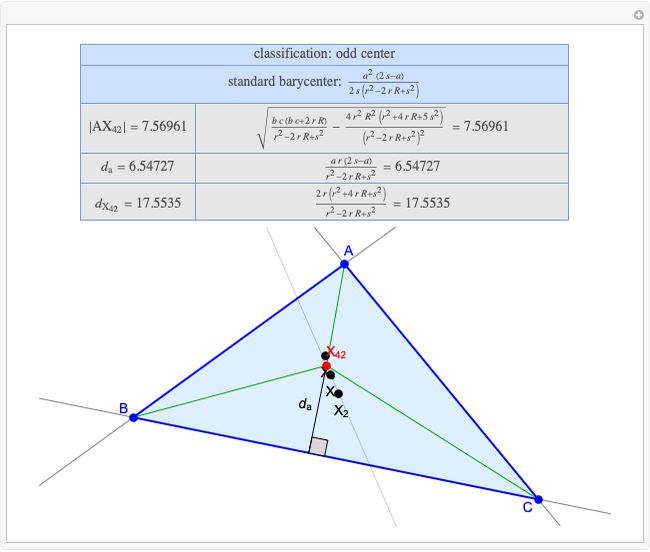
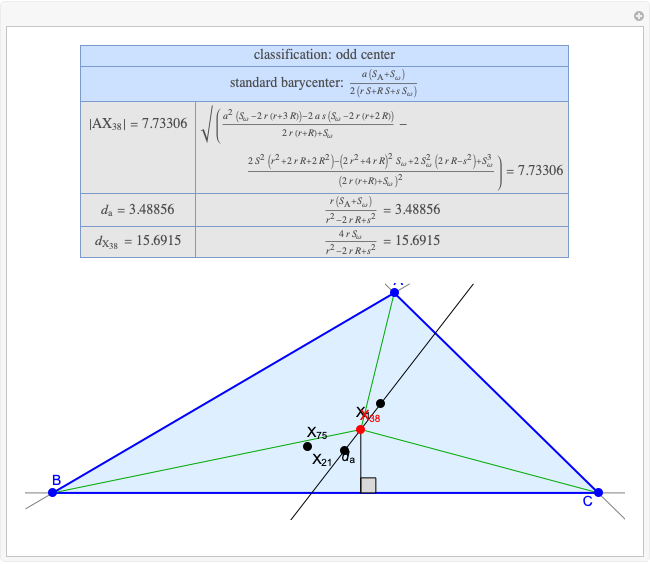
A triangle center is said to be even when its barycentric coordinates can be expressed as a function of three variables  ,
,  ,
,  that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid
that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid 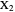 is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
Standard barycentric coordinates of a point with respect to a reference triangle have a sum of 1.
Reference
[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Sep 27, 2022) faculty.evansville.edu/ck6/encyclopedia.
Permanent Citation