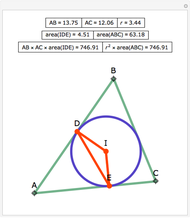
Concurrence of the Median, a Chord and a Diameter of the Incircle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
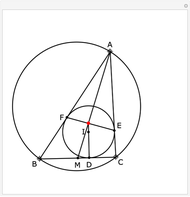
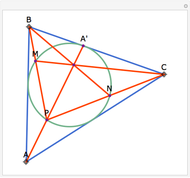
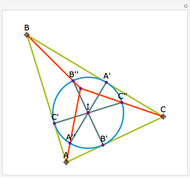
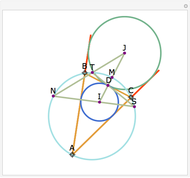
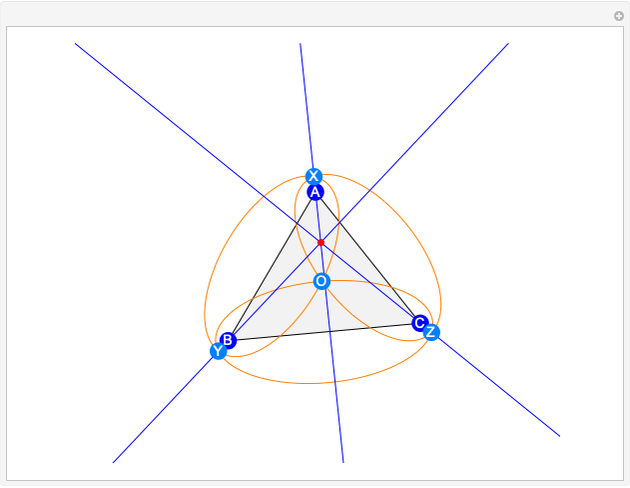
In the triangle 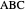 , let the incircle have center
, let the incircle have center  and let its points of tangency to the sides
and let its points of tangency to the sides  ,
, 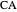 and
and 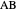 be points
be points  ,
, 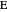 and
and 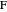 , respectively. Let
, respectively. Let 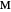 be the midpoint of
be the midpoint of 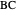 . Then the lines
. Then the lines 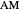 ,
, 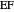 and
and  are concurrent. Drag the locators
are concurrent. Drag the locators  ,
, 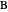 and
and  to see that this holds for any triangle.
to see that this holds for any triangle.
Contributed by: Sumith Nalabolu and Claire Wang (March 2020)
Open content licensed under CC BY-NC-SA
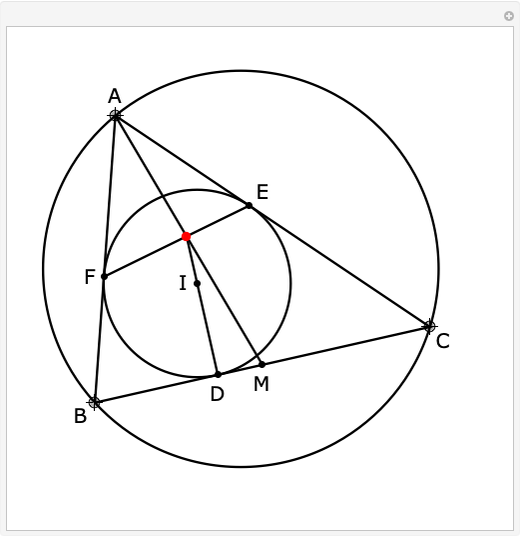
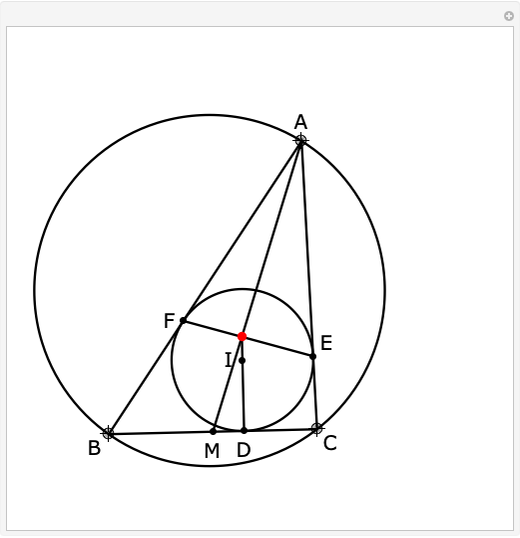
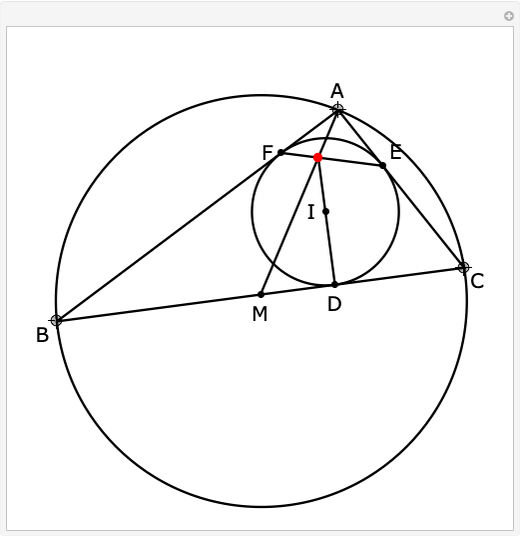
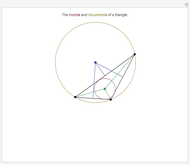
Snapshots
Details
The incircle of a triangle is the circle contained in the triangle tangent to each of the three sides. Lines are concurrent if they all pass through a common point.
See [1] for the formulas AreaOfTriangle, Circumcircle and IntersectionofLines.
See [2] for the formulas Incircle and TangencyPoint.
This was a project for Advanced Topics in Mathematics II, 2019–2020, Torrey Pines High School, San Diego, CA.
References
[1] J. Warendorff. "The Second Lemoine Circle" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheSecondLemoineCircle.
[2] J. Warendorff. "Collinearity of a Triangle's Circumcenter, Incenter, and the Contact Triangle's Orthocenter" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/CollinearityOfATrianglesCircumcenterIncenterAndTheContactTri.
Permanent Citation