Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

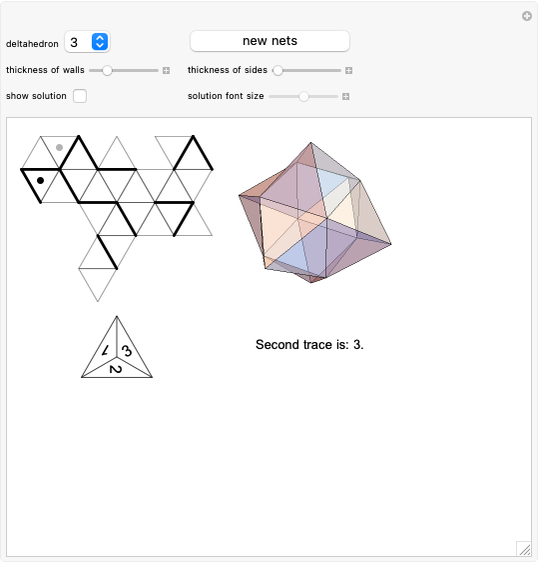
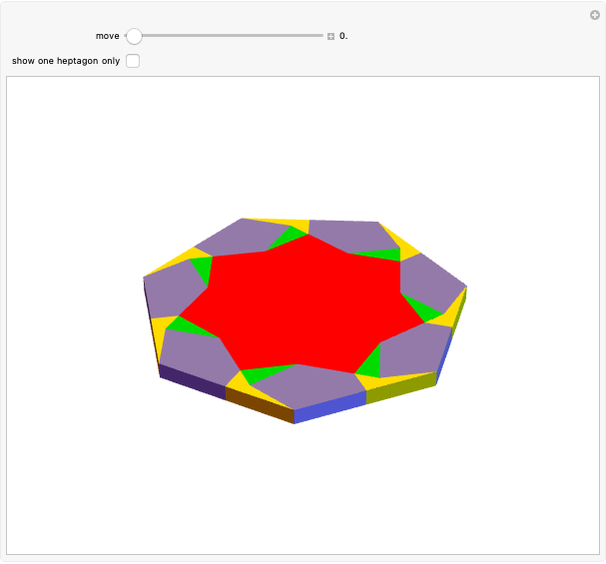
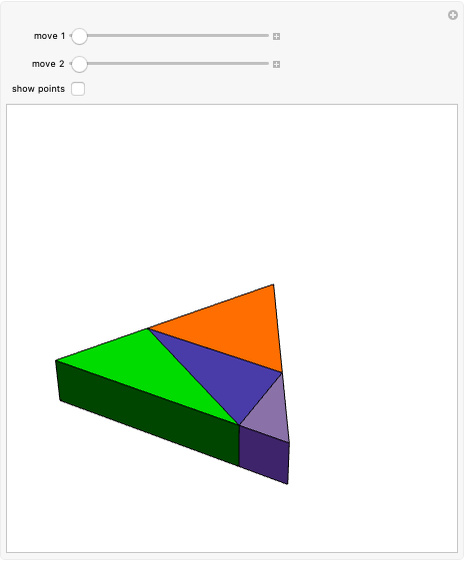
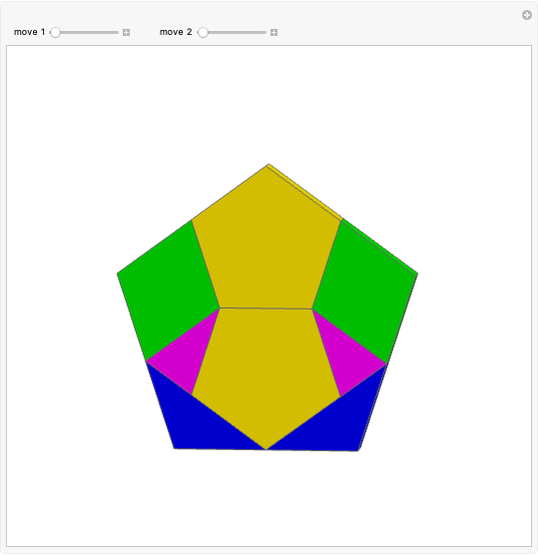
Constructing the Stewart G3 from a Triangular Hebesphenorotunda

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

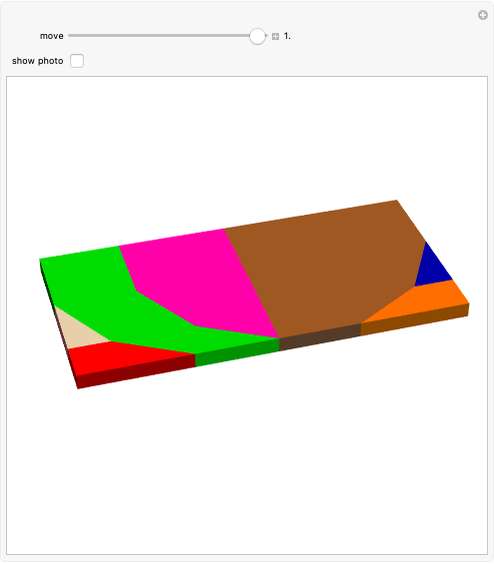
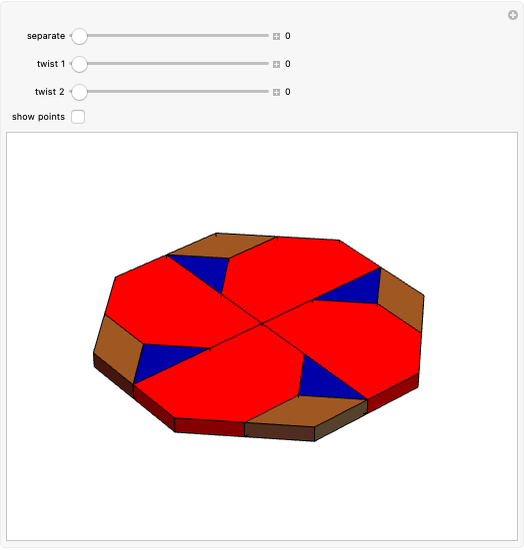
The Stewart G3 is a concave polyhedron made from seven triangles, three squares and three pentagons.

[more]

This Demonstration shows a construction of the Stewart G3 from a triangular hebesphenorotunda. We begin with a nonconvex solid consisting of five parts: the red triangular hebesphenorotunda, three brown congruent solids and a blue triangular pyramid. At the end, the four parts are a dissection of Stewart G3.

[less]

Contributed by: Izidor Hafner (January 2024)
Open content licensed under CC BY-NC-SA

Snapshots

Details

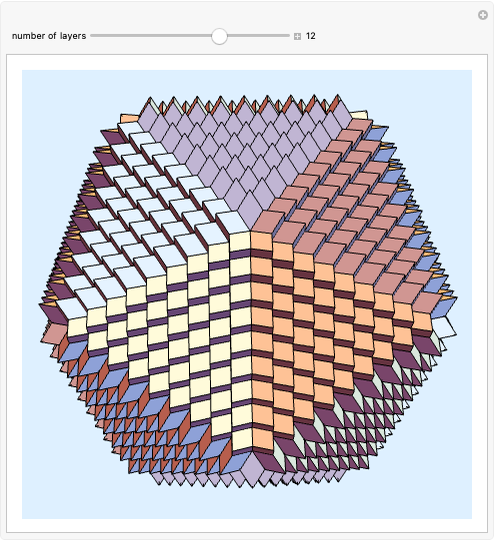
In [1] we observed that the triangular hebesphenorotunda and the Steward toroid G3 can be derived from golden rhombic solids. We also made paper models and found that these solids could be dissected into a golden rhombic solid. We made a Zometool model of such a solid.

Reference

[1] I. Hafner, "Dissection of Triangular Hebesphenorotunda, Steward Toroid, and Drilled Pentagonal Gyrobicupola," VisMath, 9(2), 2007. https://www.mi.sanu.ac.rs/vismath/hafnervisual/visual43A/Visual43A.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author

    Related Topics

Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send