Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Ellipse by Paper Folding

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

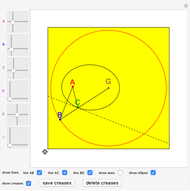
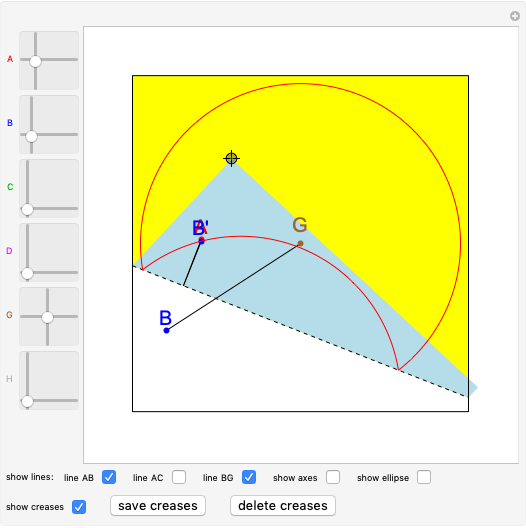
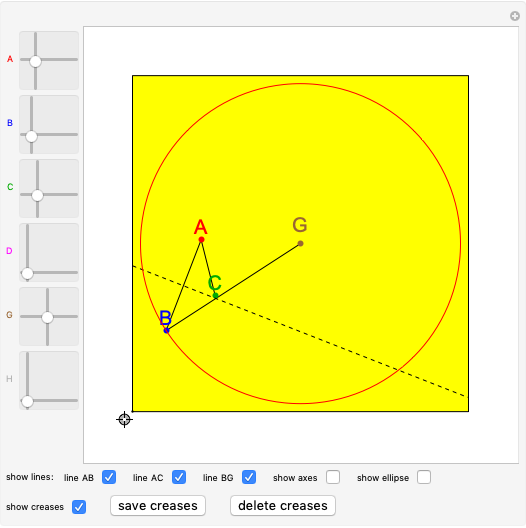
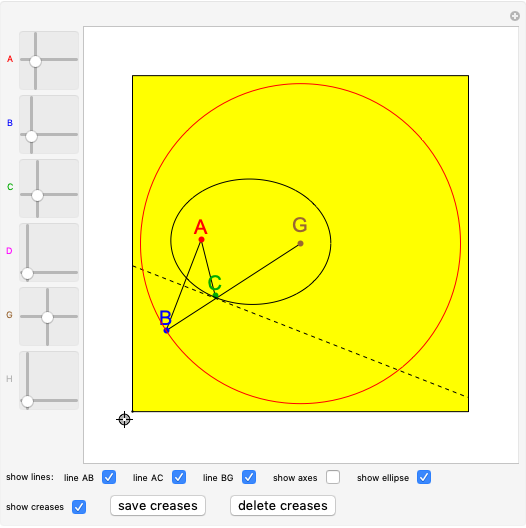
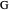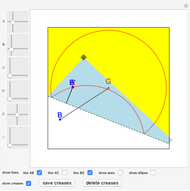
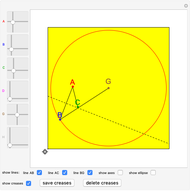
Let be the center of a circle with radius and let 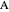be a point inside the circle. Choose a point 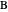on the circumference. Let 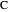be the intersection of the perpendicular bisector of 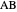and line . Then . So the point 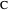is on the ellipse with foci 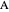and 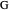and the sum of the distances from 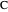to the foci is .

[more]

To construct a tangent on the ellipse, fold the circle so that the circumference touches the point .

[less]

Contributed by: Izidor Hafner (March 2019)
Using code by: Borut Levart
Open content licensed under CC BY-NC-SA

Snapshots

Details
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send