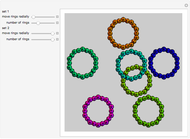
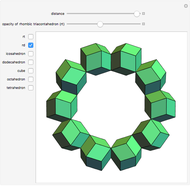
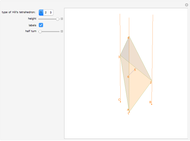
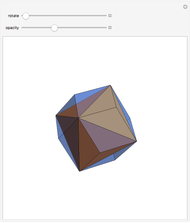
Ring of 10 Tetrahedra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
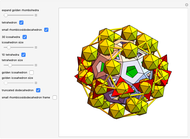
This Demonstration shows a complex figure composed of several polyhedra, including dodecahedra, golden rhombohedra, golden tetrahedra, golden octahedra, rhombic hexecontahedra, truncated dodecahedra, small rhombicosidodecahedra, icosahedra and tetrahedra. The edge length of the truncated dodecahedron is 1.
Contributed by: Sándor Kabai (May 2021)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is recommended that you operate the controls in the sequence shown.
1. The 20 golden rhombohedra of a rhombic hexecontahedron are moved radially until caught by the frame of a truncated dodecahedron. The inside vertices of the golden rhombohedra are on the vertices of a dodecahedron (edge length 1).
2. Show the tetrahedron part of the golden rhombohedra.
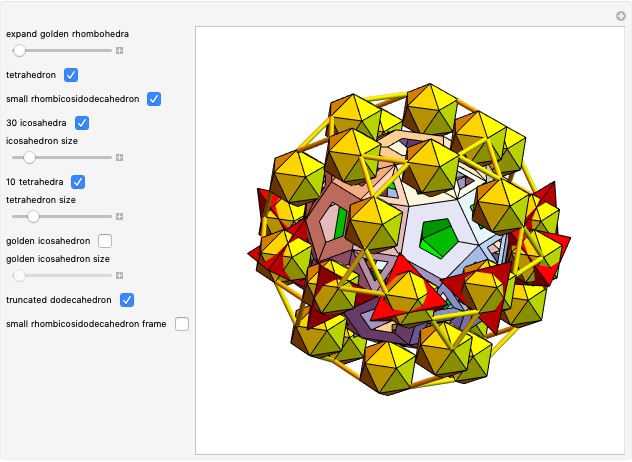
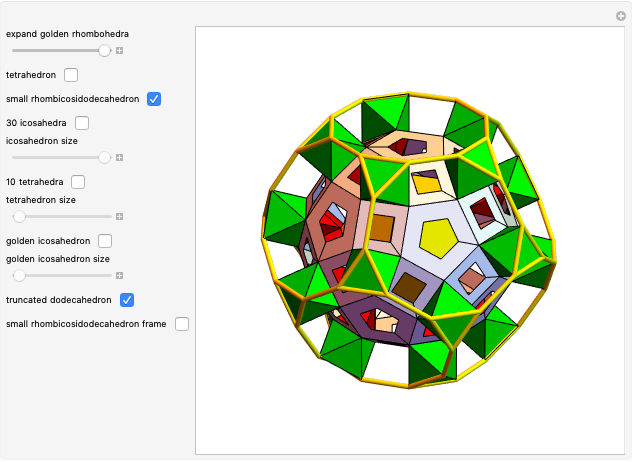
3. Show the small rhombicosidodecahedron. Now the golden octahedra are between the small rhombicosidodecahedron and the truncated dodecahedron.
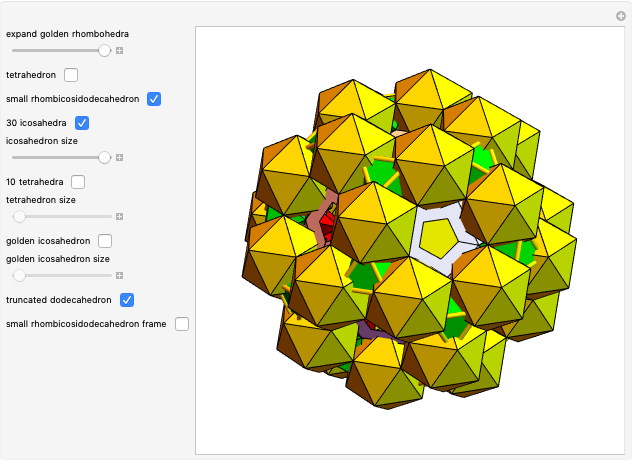
4. Insert 30 icosahedra (edge length 1) on the square faces of the small rhombicosidodecahedron. The icosahedra are connected to one another along their edges.
5. Reduce the size of the icosahedra by the golden ratio. Now the icosahedra are connected to ROs and the truncated dodecahedron at their vertices.
6. Place a ring of 10 tetrahedra on the square faces of the small rhombicosidodecahedron.
7. Increase the size of the tetrahedra by the golden ratio. Now the tetrahedra envelops the icosahedra. The vertices of the tetrahedra meet the vertices of the icosahedra. The tetrahedron/icosahedron edge ratio is the golden ratio squared multiplied by  , which equals 3.7024.
, which equals 3.7024.
8. Insert a central icosahedron having an edge length that is equivalent to the golden ratio squared. The edges meet the edges of the 30 icosahedra in the cluster.
9. Increase the size of the central icosahedron until the edge length is 2+3/golden ratio, equal to 3.8541. The faces coincide with the faces of the 30 icosahedra and the golden octahedra, and the enveloping icosahedron seems to be decorated with four triangles. The central icosahedron has an edge length of 1 (corresponding to a truncated dodecahedron), the surrounding three have an edge length of 1/golden ratio.
10. And finally, show a small rhombicosidodecahedron frame, the diagonal of its square faces coincide with the edges of tetrahedra in the ring.
Note that only 10 of the possible 30 tetrahedra are shown to allow viewing of the structure.
Permanent Citation