Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Family of Generalized Fibonacci and Lucas Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

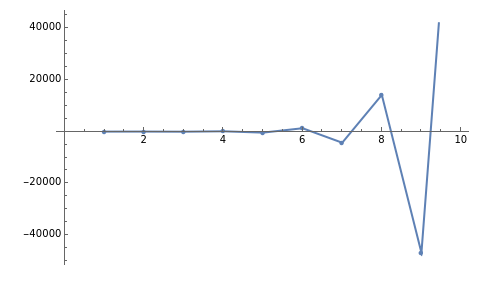
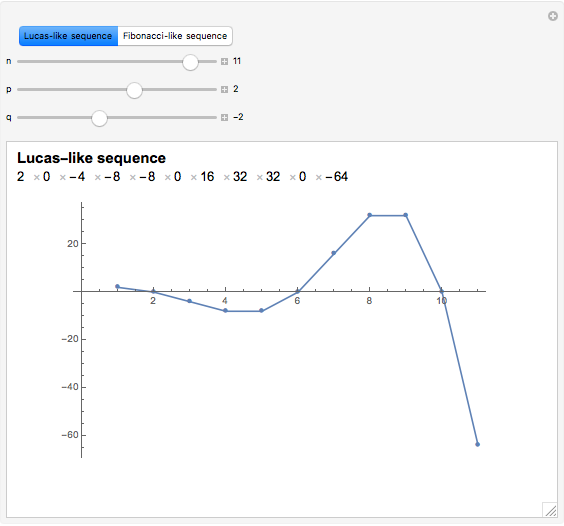
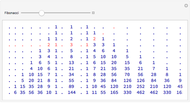
This Demonstration displays integer sequences of the form 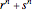and 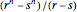, where and are the roots of the quadratic equation 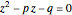with integer coefficients 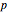and .

Contributed by: Abdulrahman Abdulaziz (June 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

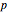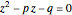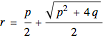If and are integers, then the roots of the quadratic equation are and .

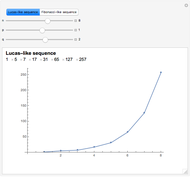
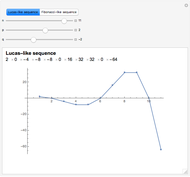
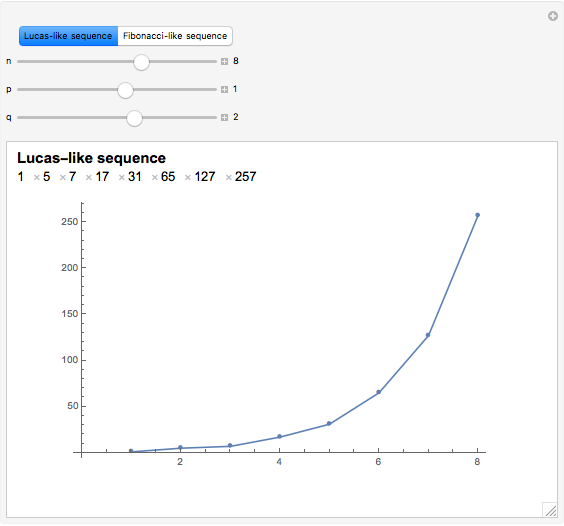
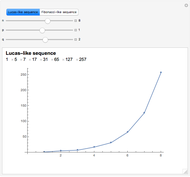
It turns out that 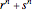produces a Lucas-like sequence, while 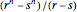produces a Fibonacci-like sequence. In particular, if 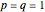, we obtain the Lucas and Fibonacci numbers.

Reference:

Integer Sequences of the Form a^n + b^n

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send