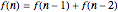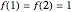Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Fibonacci and Padovan Spiral Identities

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

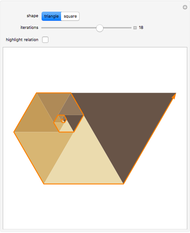
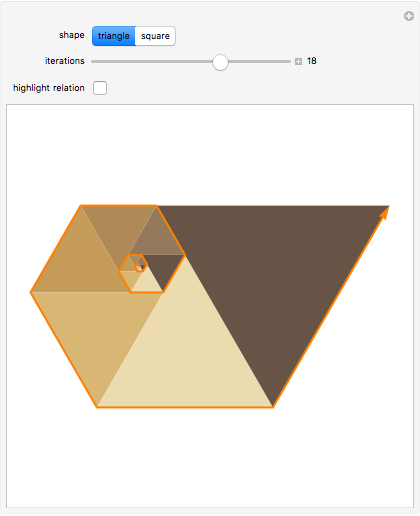
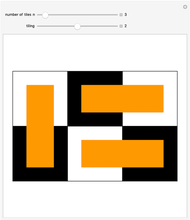
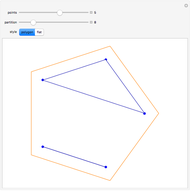
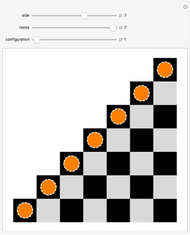
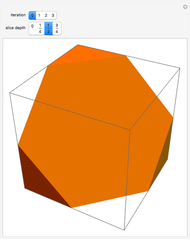
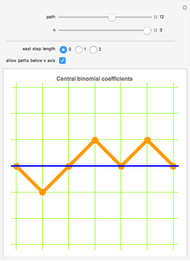
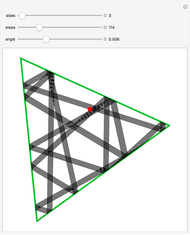
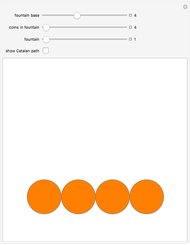
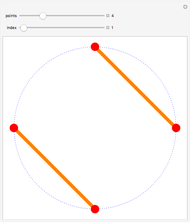
Start with an equilateral triangle with side length 1, and place a second unit triangle next to it. At each stage, moving counterclockwise around the resulting figure, construct an equilateral triangle whose base falls along the current side. The triangle side lengths match a sequence called the Padovan numbers, which are normally defined with the relation 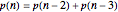, with initial conditions .

[more]

Similarly, starting with a unit square, place another unit square next to it; moving counterclockwise around the figure, construct a square with side length matching the current side of the resulting figure. The square side lengths match the Fibonacci numbers, traditionally defined with the relation , with initial conditions .

[less]

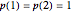Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

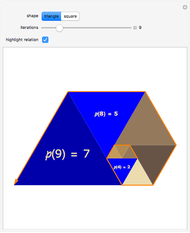
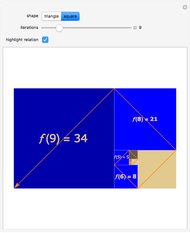
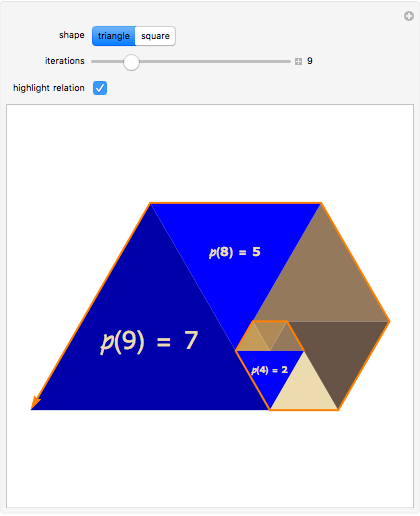
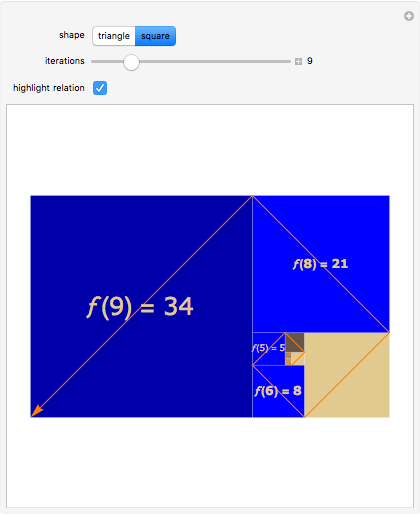
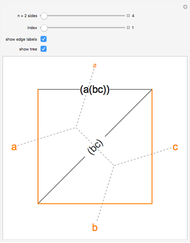
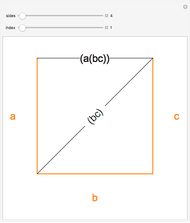
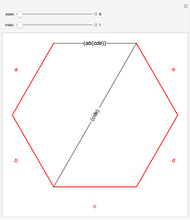
Two other relations are evident by matching up triangles or squares on opposite sides of a side.

Snapshot 1: by matching up triangle sides at each stage, the figures show that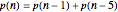

Snapshot 2: similarly, by matching up square sides, the figures show that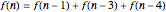

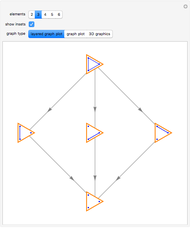
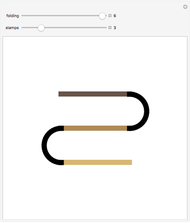
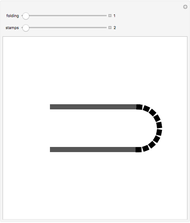
Snapshots 3, 4: hiding the relations highlights the overall construction of each shape

References

[1] M. Gardner, The Second Scientific American Book of Mathematical Puzzles and Diversions, Chicago: The University of Chicago Press, 1987, p. 93.

[2] I. Stewart, Math Hysteria: Fun and Games with Mathematics, New York: Oxford University Press, 2004, pp. 87–92.

[3] S. R. Finch, Mathematical Constants, New York: Cambridge University Press, 2003, pp. 6–9.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send