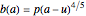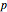Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Forest Growth Curve

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

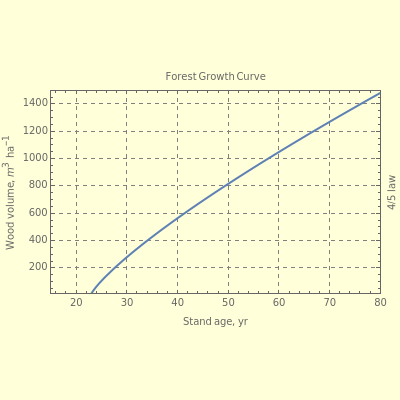
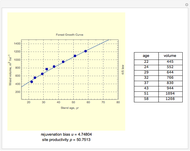
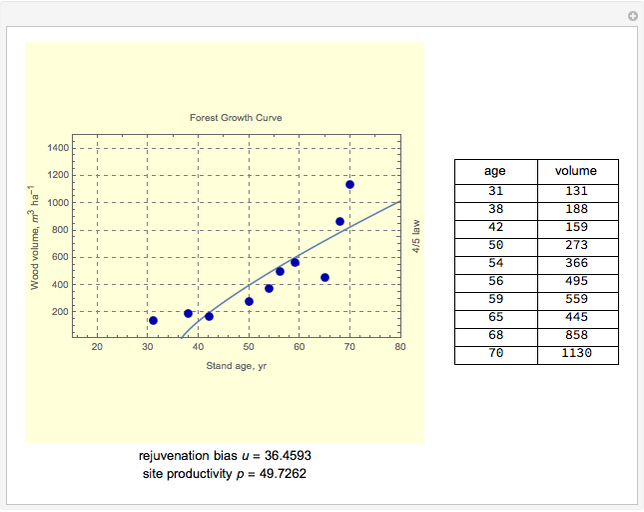
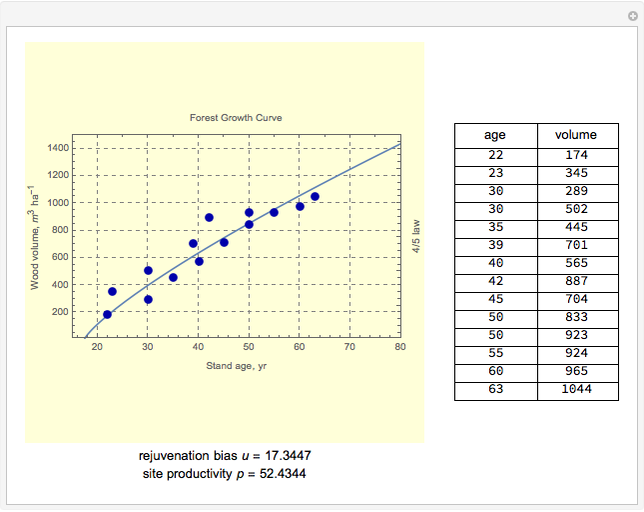
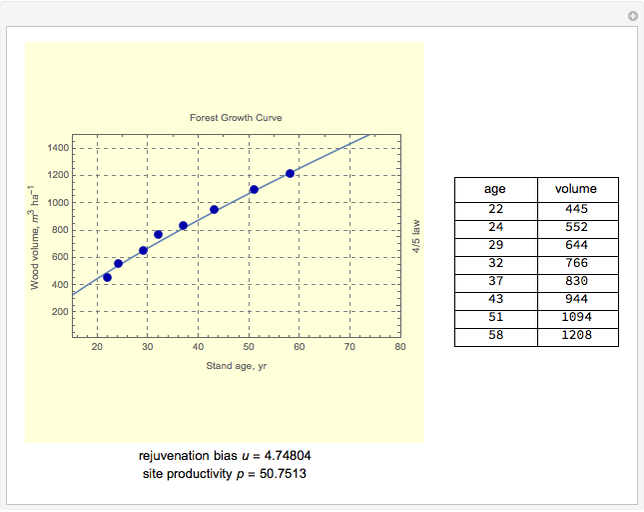
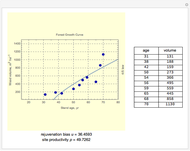
The age-dependence of forest biomass () is shown to be a power-law monomial where the power of the age () is theoretically estimated to be 4/5. However, in testing the 4/5 law against observations, a "rejuvenation bias" () should be introduced to explain the variations in growth pattern induced by delayed development or intensive thinning of the forest stand at the early stage. In other words,

[more]

,

where is characterizing site productivity. This graph shows model fits superimposed on the data from a permanent monitoring plot. It allows model testing against independent data.

[less]

Contributed by: Georgii Alexandrov (March 2011)
Additional Contributions by: Rob Morris
Open content licensed under CC BY-NC-SA

Snapshots

Details

The 4/5 law of forest growth is derived from the pipe-model theory of tree growth and the thermodynamic theory of ecological systems. Dimensional analysis, a heuristic method, is used to derive this law. This method is applied to find a verifiable physical law, not for deducing it. This Demonstration allows users to test this derived law against data from permanent monitoring plots.

The results of independent tests could be posted as readers' comments on this article.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send