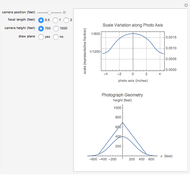
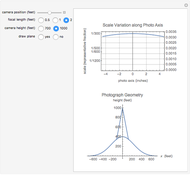
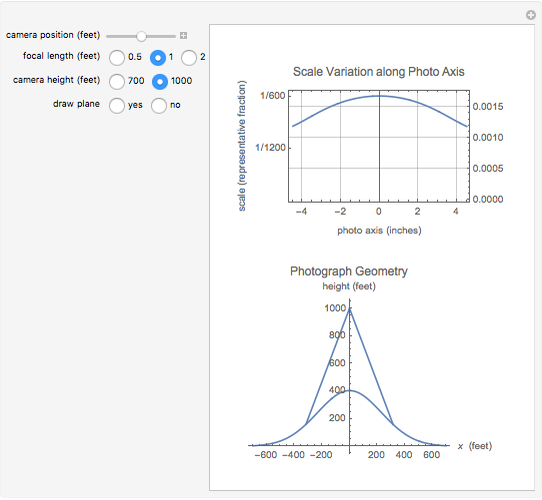
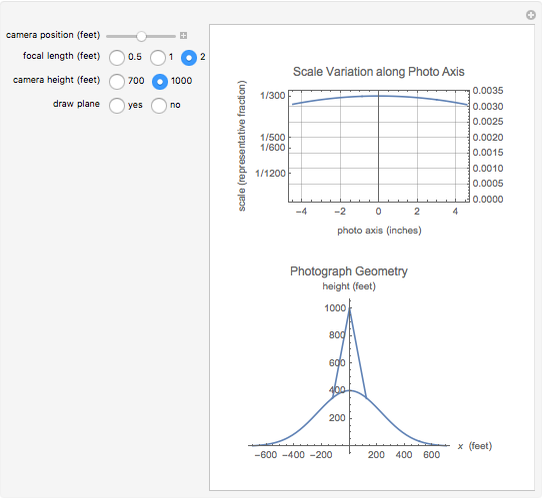
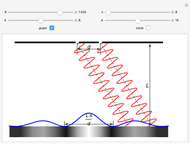
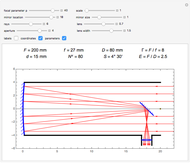
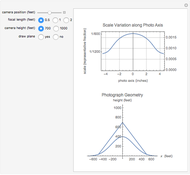
Since an aerial camera image is a perspective view, the scale of the image varies over the photograph. The upper graph shows the scale variation along the axis of a typical 9"×9" aerial photograph in the direction of flight. The labels on the vertical axis of the graph are the scale of the photo in representative fraction form on the left and decimal form on the right. The gridlines are equal increment changes in the decimal form of the scale. On the lower graph, a normal distribution is used to represent the ground surface. The ground surface between the two intersecting ray tracing lines is the area covered by the photo. The image of the plane can be turned on or off. The scale variation is shown as a function of the position of the camera, focal length of the camera, and the vertical distance from the surface to the camera.