Binomial Approximation to a Hypergeometric Random Variable

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
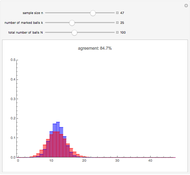
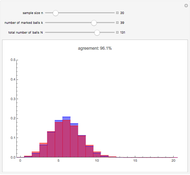
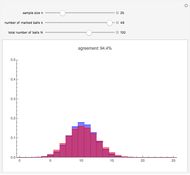
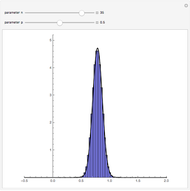
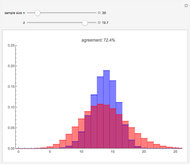
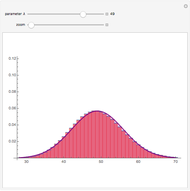
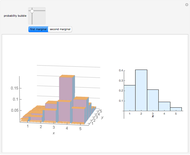
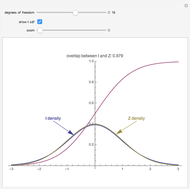
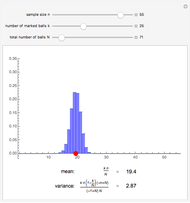
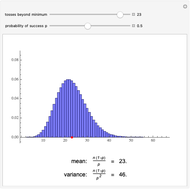
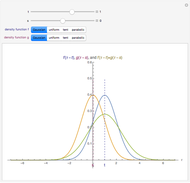
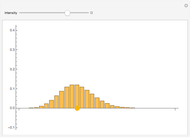
If  balls are sampled from a bin containing
balls are sampled from a bin containing 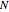 balls of which
balls of which  are marked, then the distribution of the number of marked balls in the sample depends on whether the sampling is done with or without replacement.
are marked, then the distribution of the number of marked balls in the sample depends on whether the sampling is done with or without replacement.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Binomial Approximation to a Hypergeometric Random Variable"
http://demonstrations.wolfram.com/BinomialApproximationToAHypergeometricRandomVariable/
Wolfram Demonstrations Project
Published: March 7 2011