Birds on a Wire

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
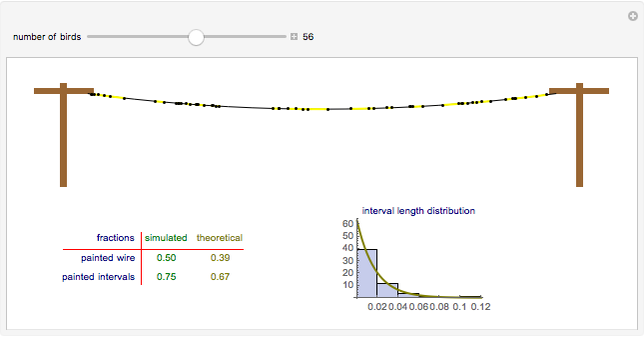
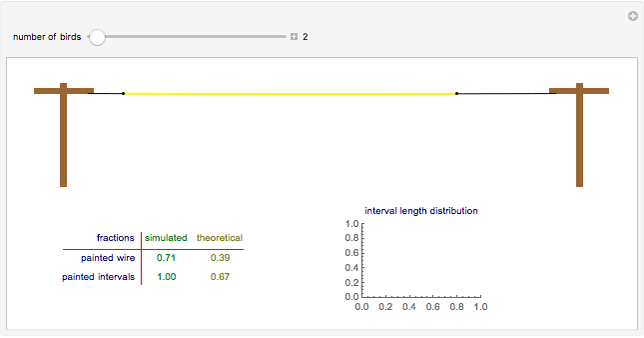
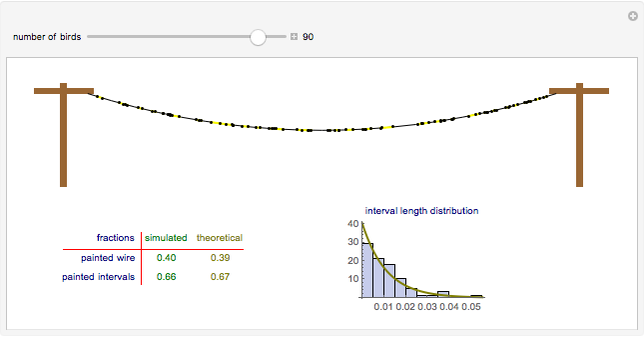
A number of birds randomly land on a telephone wire. If the intervals between each bird and its closest companion were painted, what would be the expected fraction of wire painted? And what proportion of the number of intervals would be painted? The key to answering these questions is to realize that the probability distribution of interval lengths is (approximately) exponential. Knowing that, these fractions can be calculated to be 7/18 and 2/3.
Contributed by: Jacqueline D. Wandzura and Stephen M. Wandzura (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This problem was inspired by Birds on a Wire.
If the mean density of birds is 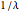 , then the probability distribution of interval lengths
, then the probability distribution of interval lengths 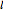 is
is 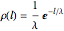 . Integrating this, the probability that an interval is less than
. Integrating this, the probability that an interval is less than 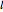 is
is  . Squaring that gives the probability that the two intervals on either side of a chosen interval are both smaller than the chosen interval, in which case it would not be painted. Thus, the probability that an interval of length
. Squaring that gives the probability that the two intervals on either side of a chosen interval are both smaller than the chosen interval, in which case it would not be painted. Thus, the probability that an interval of length 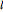 will be painted is
will be painted is 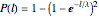 . Thus, the probability that a link will be painted is
. Thus, the probability that a link will be painted is 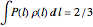 . Likewise, the average length of an interval weighted by the probability that it is painted is
. Likewise, the average length of an interval weighted by the probability that it is painted is 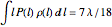 . Dividing by the average length of an interval λ gives the fraction of painted wire as
. Dividing by the average length of an interval λ gives the fraction of painted wire as 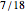 .
.
Permanent Citation
"Birds on a Wire"
http://demonstrations.wolfram.com/BirdsOnAWire/
Wolfram Demonstrations Project
Published: March 7 2011