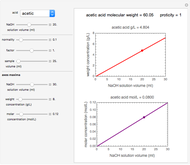
Distribution of the Means of Samples Having Random Sizes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
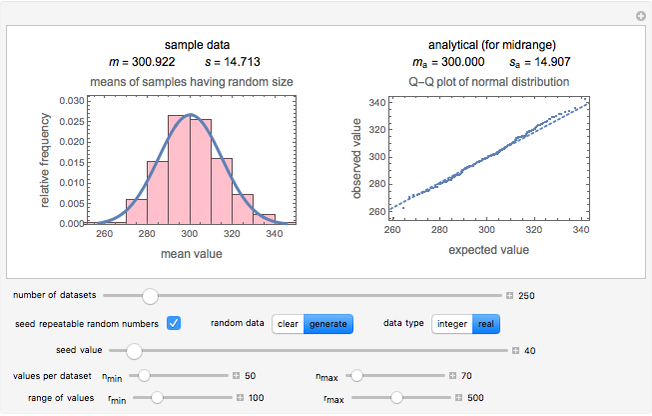
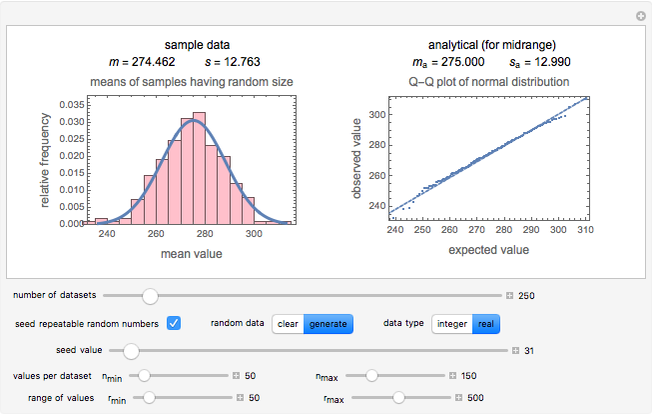
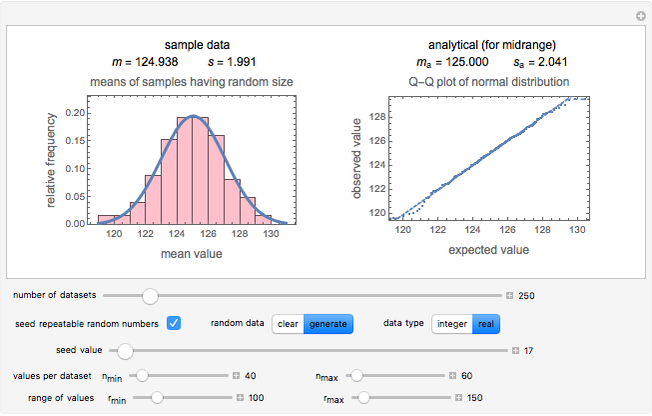
This Demonstration generates a specified number of random samples of real numbers or integers taken from a population having uniform distribution within a chosen range; the sample sizes are also chosen at random from a uniform distribution with specified range. The Demonstration calculates the means of the samples and plots their histogram with a superimposed normal (Gaussian) probability density function having its mean and standard deviation equal to the mean and standard deviation of the means of the random samples.
[more]
Contributed by: Mark D. Normand, Joseph Horowitz, and Micha Peleg (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details

The original central limit theorem (CLT) states that under certain conditions, the mean of a random sample of 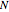 numbers has an approximately normal (Gaussian) distribution as the sample size
numbers has an approximately normal (Gaussian) distribution as the sample size 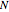 approaches infinity. According to theorems proven by Robbins [1] and Billingsley [2] (see [3]), normality will be approached even if the sample size
approaches infinity. According to theorems proven by Robbins [1] and Billingsley [2] (see [3]), normality will be approached even if the sample size 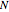 is random, provided that it is sufficiently large and its distribution sufficiently narrow. This Demonstration is intended to show that the means of samples of uniformly distributed random numbers, of random sample sizes, indeed have an approximately normal distribution if the sample sizes are sufficiently large and picked from a uniform distribution, and that they become closer to being normally distributed if the sample size range narrows.
is random, provided that it is sufficiently large and its distribution sufficiently narrow. This Demonstration is intended to show that the means of samples of uniformly distributed random numbers, of random sample sizes, indeed have an approximately normal distribution if the sample sizes are sufficiently large and picked from a uniform distribution, and that they become closer to being normally distributed if the sample size range narrows.
You can select with sliders both the size limits, 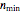 and
and 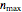 , of the random samples, and the range,
, of the random samples, and the range, 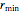 and
and  , from which the random numbers are to be chosen. The program then generates samples of random numbers within the specified limits and plots the histogram of the mean values of these samples. It calculates a corresponding normal distribution having the same mean,
, from which the random numbers are to be chosen. The program then generates samples of random numbers within the specified limits and plots the histogram of the mean values of these samples. It calculates a corresponding normal distribution having the same mean, 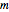 , and standard deviation,
, and standard deviation,  , as those of the generated means, and plots its probability density function superimposed on the histogram. For comparison, the program also calculates the analytical mean,
, as those of the generated means, and plots its probability density function superimposed on the histogram. For comparison, the program also calculates the analytical mean,  , and standard deviation,
, and standard deviation, 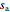 , of the normal distribution had the sets been of uniform of size
, of the normal distribution had the sets been of uniform of size 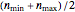 . It plots the corresponding Q-Q plot for visual inspection of the normality of the generated data's distribution.
. It plots the corresponding Q-Q plot for visual inspection of the normality of the generated data's distribution.
References
[1] H. E. Robbins, "The Asymptotic Distribution of the Sum of a Random Number of Random Variables," Bulletin of the American Mathematical Society, 54(12), 1948 pp. 1151–1161. projecteuclid.org/euclid.bams/1183513324.
[2] P. Billingsley, "Limit Theorems for Randomly Selected Partial Sums", Annals of Mathematical Statistics 33(1), 1962 pp. 85–92. projecteuclid.org/euclid.aoms/1177704713.
[3] W. Feller, An introduction to Probability Theory and Its Application, 2nd ed., Vol. II, New York: John Wiley & Sons, 1971.
[4] Wikipedia. "Q-Q Plot." (Sep 7, 2012) en.wikipedia.org/wiki/Q% E2 %80 %93 Q_plot.
Permanent Citation