Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

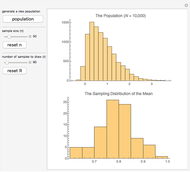
Birthday Paradox Probability Estimates

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

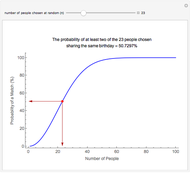
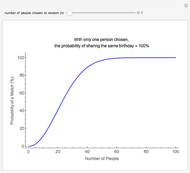
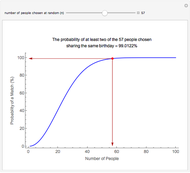
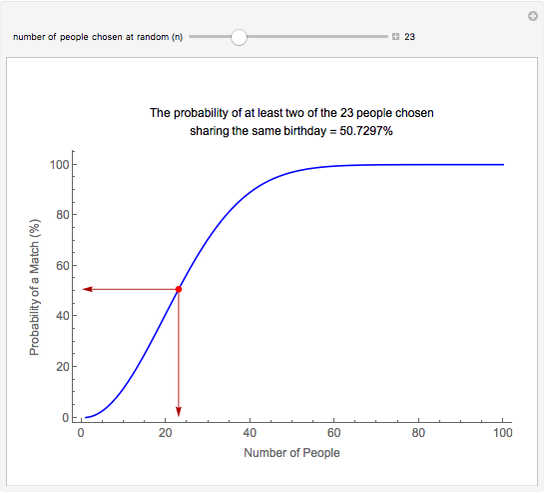
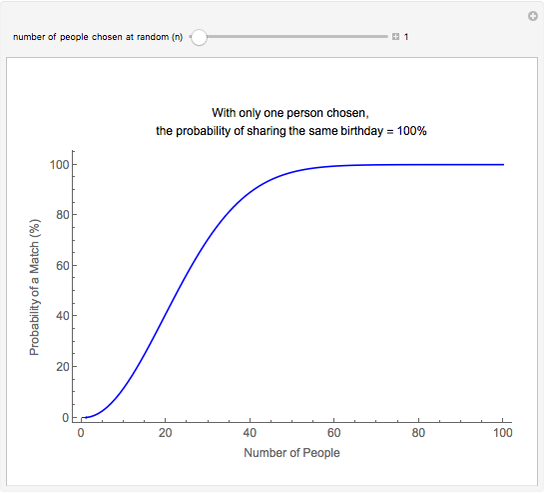
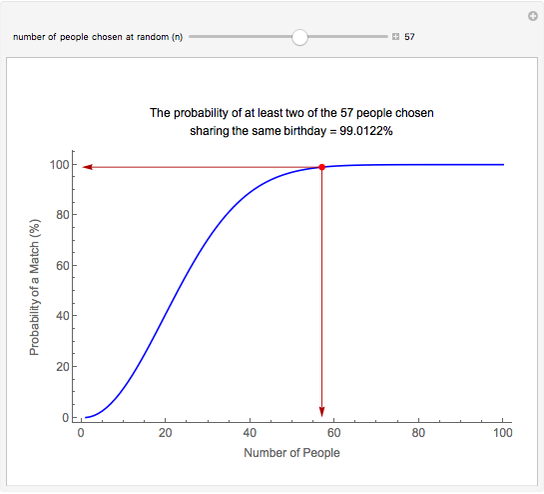
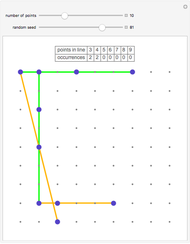
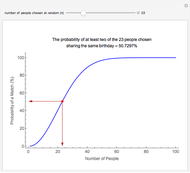
This Demonstration of the birthday problem shows the probability that at least two individuals share the same birthday assuming that there are 365 equally likely possible birthdays.

[more]

You may be surprised to find that if you randomly select 23 people there is just over a 50% probability that at least two of the individuals will share the same birthday. Move the slider to add more people and see how the probability increases. At around 57 people you should find the probability of a match reaches approximately 99%.

[less]

Contributed by: Scott R. Colwell (August 2011)
Open content licensed under CC BY-NC-SA

Details

The formula for the probability of some people out of to share the same birthday is:

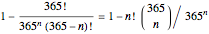, where 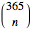is a binomial coefficient.

Reference

[1] E. H. McKinney, "Generalized Birthday Problem," The American Mathematical Monthly, 73(4), 1966 pp. 385–387.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send