Chain Length Distribution of Polymers after Degradation by Random Chain Scission

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
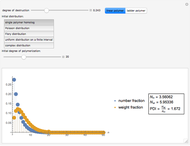
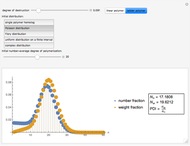
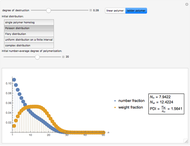
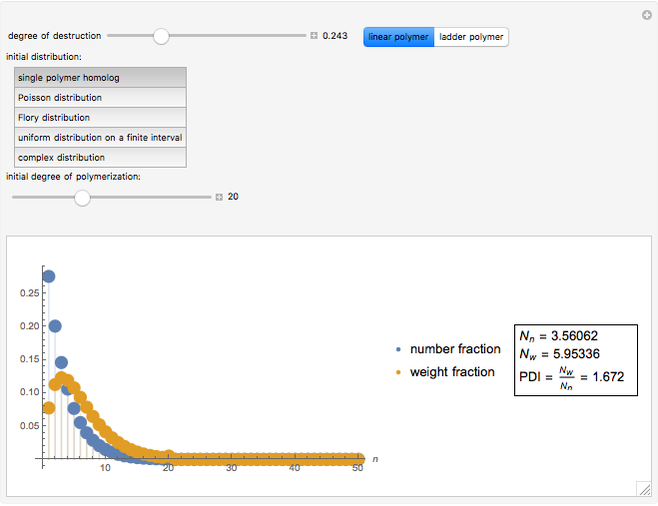
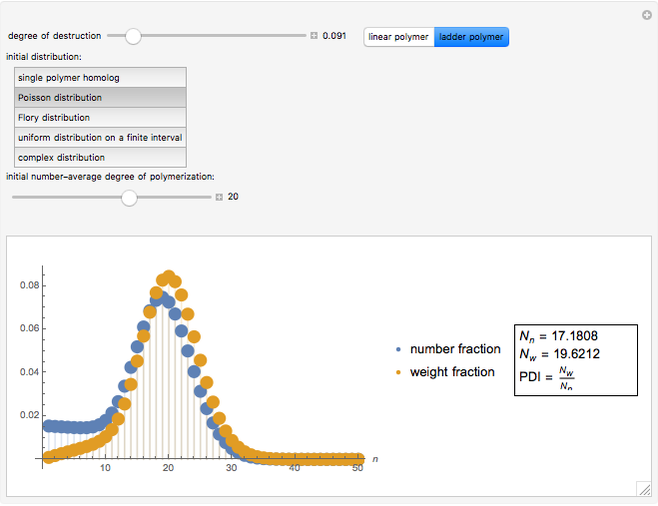
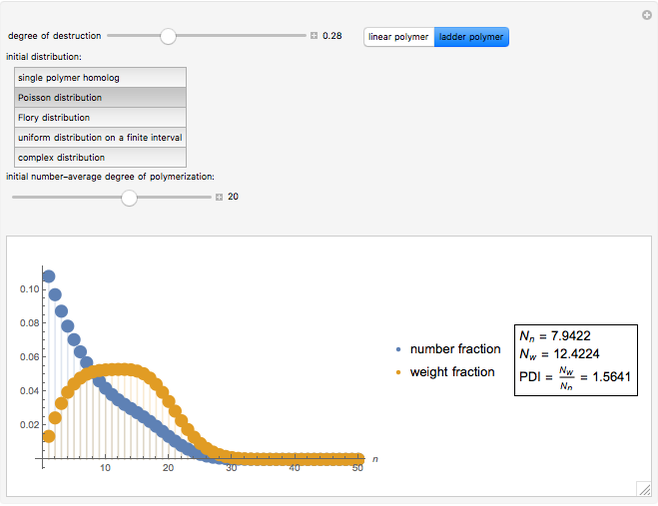
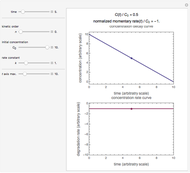
This Demonstration shows a simulation of the chain length distribution after the destruction of a polymer by random chain breaking. Move the slider "degree of destruction" to 0, set the initial distribution and observe the distribution change at different degrees of destruction.
Contributed by: A. A. Koledenkov (February 2019)
Open content licensed under CC BY-NC-SA
Details
The kinetics of the process of random chain breaking for linear polymers is described by the equation:
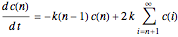 ,
,
where 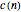 is the molar concentration of
is the molar concentration of  -mer and
-mer and  is the first-order rate constant for chain-breaking reaction.
is the first-order rate constant for chain-breaking reaction.
For a monodisperse polymer with boundary condition 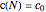 , the general solution of this equation is:
, the general solution of this equation is:
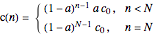 ,
,
where 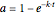 is the fraction of broken bonds, or the degree of destruction.
is the fraction of broken bonds, or the degree of destruction.
Normalization gives the numerical distribution function:
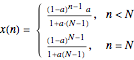
In case of complex initial distributions, the absence of mutual influence of the chains makes it possible to apply this distribution function to each polymer homolog, taking into account its concentration in the initial polymer.
A special solution for the initial Flory distribution, since the random chain breaking does not change the nature of the distribution:
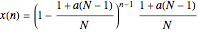 ,
,
where  is the molar fraction of
is the molar fraction of  -mer and
-mer and 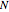 is the number-average degree of polymerization of the starting polymer.
is the number-average degree of polymerization of the starting polymer.
For ladder polymers with monodisperse initial distribution:
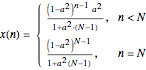 ,
,
where  is the probability of double-stranded break at a degree of destruction
is the probability of double-stranded break at a degree of destruction  .
.
Based on the chain length distribution, the number-average degree of polymerization 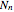 , the weight-average degree of polymerization
, the weight-average degree of polymerization 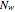 and the polydispersity index
and the polydispersity index 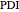 are calculated:
are calculated:
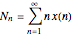 ,
,
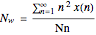 ,
,
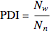 .
.
Snapshots
Permanent Citation