Chiral Tunneling and the Klein Paradox in Graphene

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
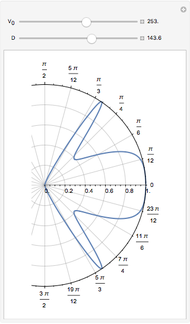
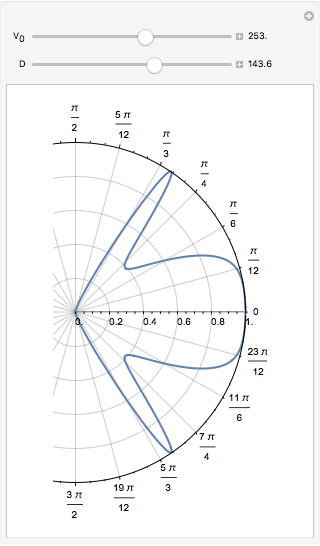
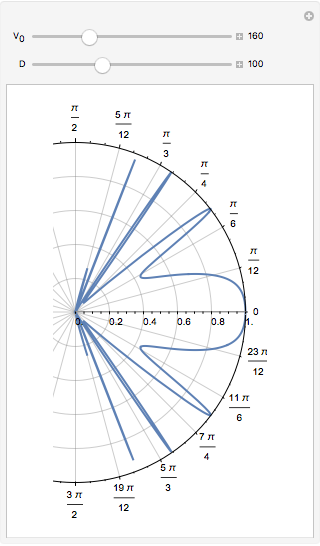
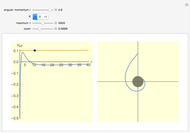
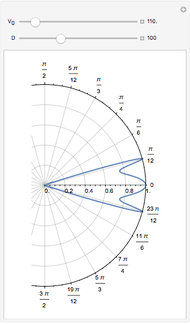
This plot shows the transmission coefficient for a barrier of height 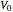 in graphene as a function of the angle of a plane wave incident on the barrier.
in graphene as a function of the angle of a plane wave incident on the barrier.
Contributed by: Niels Walet (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This is a minor generalization of the plot shown in Fig. 2a of [1]. It shows the transmission coefficient for a plane wave incident on a barrier of height 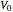 . The parameters for graphene given in that paper have been used: Dirac speed
. The parameters for graphene given in that paper have been used: Dirac speed  , energy
, energy 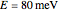 , Fermi momentum
, Fermi momentum 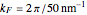 ; the width of barrier
; the width of barrier  ranges from
ranges from 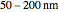 and
and 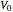 lies between
lies between 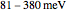 .
.
M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, "Chiral Tunneling and the Klein Paradox in Graphene," Nature Phys., 2, 2006 pp. 620–625.
Permanent Citation