The Causal Interpretation of Quantum Tunneling through a Square Barrier and Well

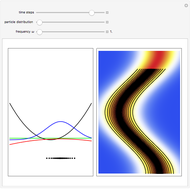
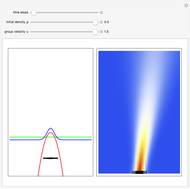
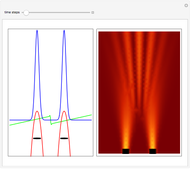
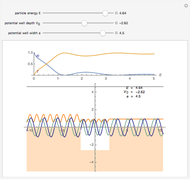
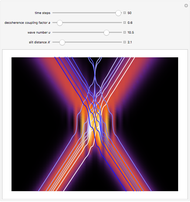
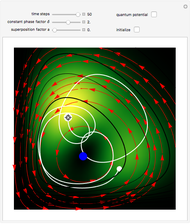
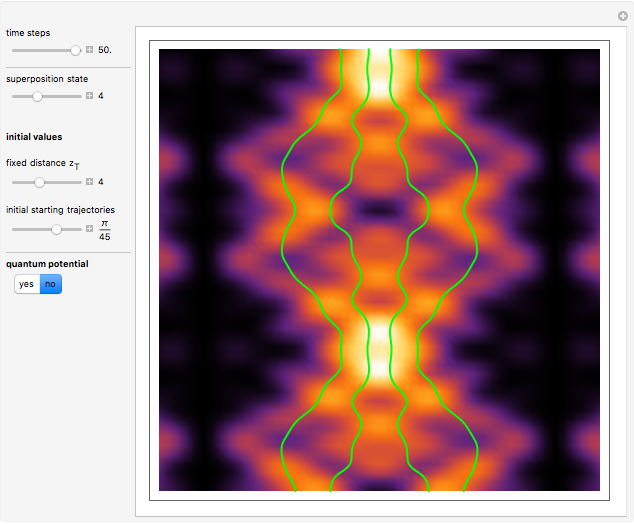
In 1967 Goldberg, Schey, and Schwartz created one of the first computer-generated images of the scattering of Gaussian wave packets off wells and barriers as described by the time-dependent Schrödinger equation with the potential term . This Demonstration reproduces their results in the causal interpretation of quantum theory, which was first accomplished by Dewdney and Hiley. While distinctly non-Newtonian, Bohmian mechanics is a fully deterministic theory of particles in motion in terms of individual processes, but the trajectories are not detectable directly. The interaction of the Gaussian packet with the barrier or well leads to reflected and transmitted packets (the potential acts as a beam splitter). After the interaction between the Gaussian wave and the potential, the wave packet approaches the Gaussian form more and more closely as it evolves in time. The fate of a particle depends sensitively on its position, but in general, it is not possible to control the initial position of the particle in the wave packet. In the case of the barrier/well one finds that in addition to reflection and transmission there is a finite probability of a particle being trapped inside the barrier (or well) for a finite time. During the scattering process an "Airy wave packet" pattern is observed that spreads out as it propagates. The parameters in this Demonstration are chosen so that the dispersion of the Gaussian packet is clearly seen. The initial positions of the particles are linearly distributed around the peak of the packet inside the wave. 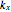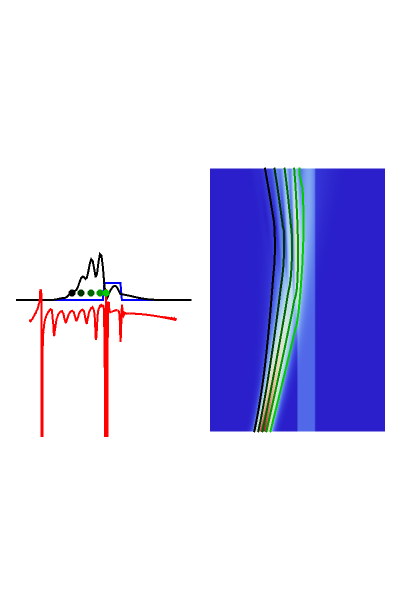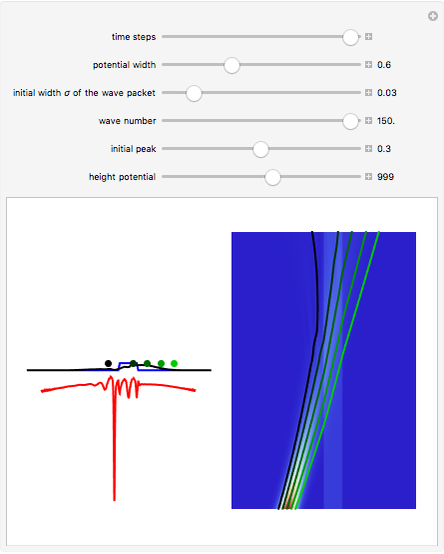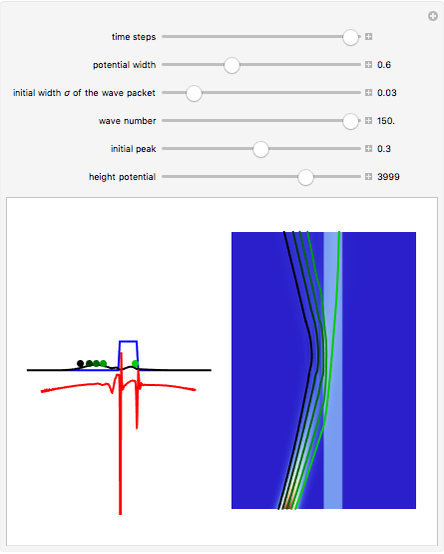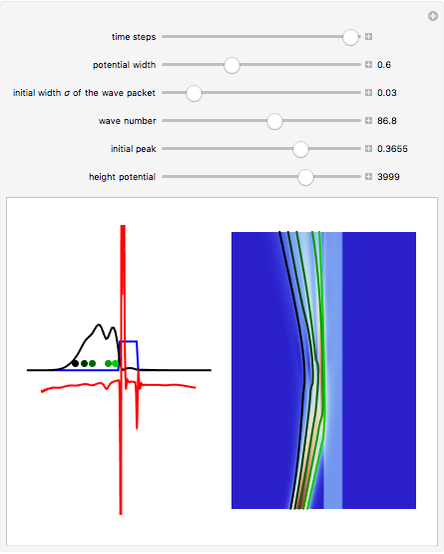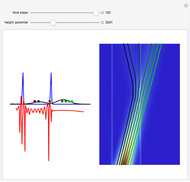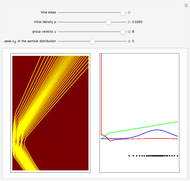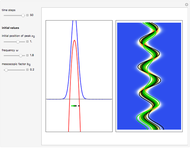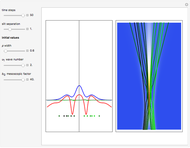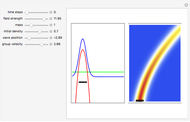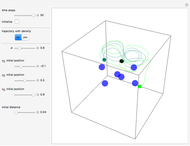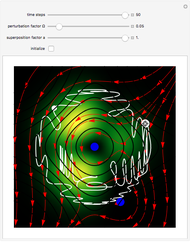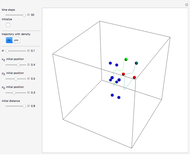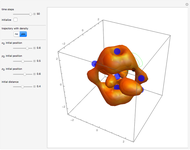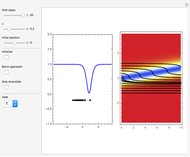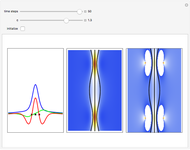The initial unnormalized wave is , with and where governs the initial width of the wave packet and is the wave number. The trajectories are positioned in 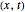(, ) space. The graphic on the right shows the squared wavefunction, the potential (blue), and the trajectories. The graphic on the left shows the particles' positions, the squared wavefunction (black), and the potential (blue). In the program, if AccuracyGoal, PrecisionGoal, and MaxSteps are increased, the results (wave packets and trajectories) will be more accurate and the quantum potential will be computable.