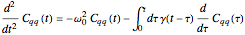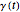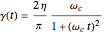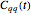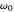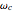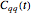Classical Correlation Function via Generalized Langevin Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
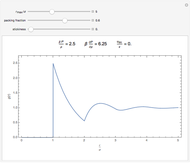
This Demonstration calculates the position-position correlation function 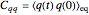 , where
, where 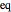 stands for "averaged over thermal equilibrium" for a system consisting of a harmonic oscillator with frequency
stands for "averaged over thermal equilibrium" for a system consisting of a harmonic oscillator with frequency 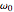 , coupled to a harmonic bath whose spectral density is ohmic with cutoff frequency
, coupled to a harmonic bath whose spectral density is ohmic with cutoff frequency 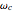 and friction
and friction  , by solving the generalized Langevin equation numerically:
, by solving the generalized Langevin equation numerically:
Contributed by: Yifan Lai (May 2018)
Additional contributions by: Eitan Geva (University of Michigan)
Open content licensed under CC BY-NC-SA
Details
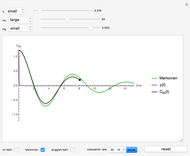
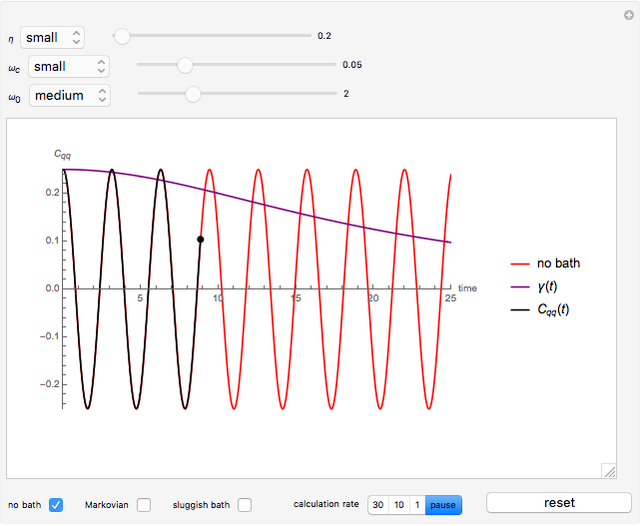
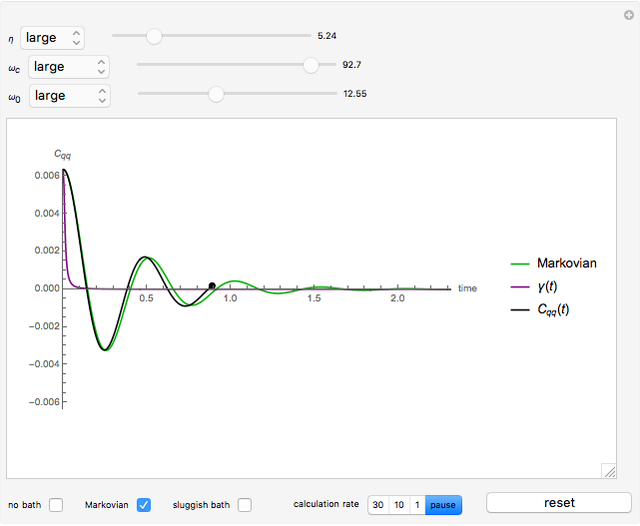
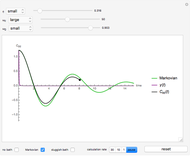
Snapshot 1: the behavior of the system when the system-bath coupling is very small
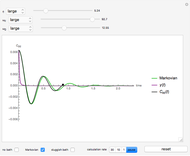
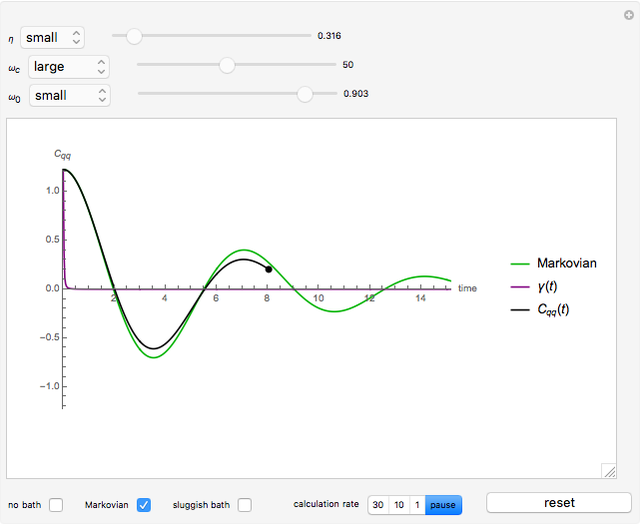
Snapshot 2: the behavior of the system at the Markovian limit
Snapshot 3: the behavior of the system at the sluggish bath limit
Controls
Toggle the display for the three approximations at the lower left. Drag the sliders on top to change the value of the three parameters, and the plot changes accordingly. You can change the range of the sliders using the popup menus to the left of the sliders. After necessary adjustments to the parameters, click the "begin calculation" button at the bottom right to begin the numeric calculation, during which the parameters can no longer be changed. The calculation rate can be toggled or paused using the setter bar at the bottom; a setting of 10 is highly recommended. After the calculation, click "reset" to discard the numeric result, and the parameters can be altered again.
Mathematical Details
All positions and momentum are mass-weighted (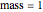 ),
), 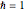 ,
,  .
.
The Hamiltonian of the system is given by
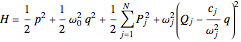 ,
,
where 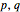 are the position and momentum of the system and
are the position and momentum of the system and 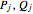 are the position and momentum of the
are the position and momentum of the 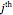 bath mode. The system-bath coupling coefficient
bath mode. The system-bath coupling coefficient 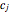 is given by the ohmic spectral density
is given by the ohmic spectral density 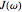 :
:
 .
.
The position-position correlation function 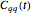 can be derived in closed form for the bath-free Hamiltonian:
can be derived in closed form for the bath-free Hamiltonian:
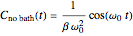 .
.
Markovian limit:
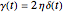 .
.
 ,
,
where

can be imaginary.
The sluggish bath limit is
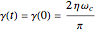 ,
,
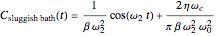 ,
,
where
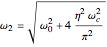 .
.
Reference
[1] A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems, New York: Oxford University Press, 2006.
Submission from the Compute-to-Learn course at the University of Michigan.
Snapshots
Permanent Citation